题目内容
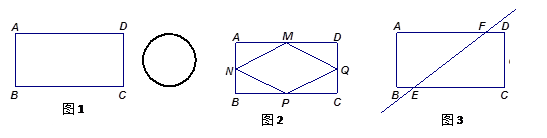
如图甲,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不运动至M,C),以AB为直径作⊙O,过点P的切线交AD于点F,切点为E。

(1)求四边形CDFP的周长;(3分)
(2)请连结OF,OP,求证:OF⊥OP;(4分)
 (3)延长DC,FP相交于点G,连结OE并延长交直线DC于H(如图乙).是否存在点P
(3)延长DC,FP相交于点G,连结OE并延长交直线DC于H(如图乙).是否存在点P
使△EFO∽△EHG(其对应关系是 )?如果存在,试求此时的BP的长;如果不存在,请说明理由。(5分)

(1)求四边形CDFP的周长;(3分)
(2)请连结OF,OP,求证:OF⊥OP;(4分)
 (3)延长DC,FP相交于点G,连结OE并延长交直线DC于H(如图乙).是否存在点P
(3)延长DC,FP相交于点G,连结OE并延长交直线DC于H(如图乙).是否存在点P使△EFO∽△EHG(其对应关系是 )?如果存在,试求此时的BP的长;如果不存在,请说明理由。(5分)
(1)6(2)证明见解析(3)存在,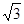
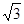
解:(1)∵四边形ABCD是正方形 ∴∠A=∠B=Rt∠ ∴AF、BP都是⊙O的切线 (1分)
又∵PF是⊙O的切线 ∴EF=FA,PE=PB ∴四边形CDFP的周长为AD+DC+CB=2×3="6" (3分)
(2)∴连结OE,∵PF是⊙O的切线 ∴OE⊥PF .
在Rt⊿AOF和Rt⊿EOF中∵AO=EO,OF=OF ∴Rt⊿AOF∽Rt⊿EOF∴∠AOF=∠EOF(5分)
同理∠BOP=∠EOP ∴∠EOF+∠EOP=1/2×180°=90°∴∠EOP=90°即OF⊥OP (7分)
(3)存在(如果这一步不写,但下面各步骤都正确,不扣分) (8分)
∵∠EOF=∠AOF ∴∠EHG=∠AOE=2∠EOF,
∴当∠EHG=∠AOE=2∠EOF,即∠EOF=30°时 Rt⊿EOF∽Rt⊿EHG (10分)
此时∠EOF=30°,∠BOP=∠EOP=90°-30°=60°
∴BP=OB·tan60°=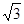 (12分)
(12分)
(1)根据切线的性质,将所求四边形CDFP的边转化为已知正方形ABCD的边,即可求得;
(2)连结OE,根据切线的性质和相似三角形,求得∠EOP=90°,即可求得OF⊥OP;
(3)要△EFO∽△EHG,必须∠EHG=∠EFO=2∠EOF=60°,在直角△OBP中,由正切定理可求出BP的长.
又∵PF是⊙O的切线 ∴EF=FA,PE=PB ∴四边形CDFP的周长为AD+DC+CB=2×3="6" (3分)
(2)∴连结OE,∵PF是⊙O的切线 ∴OE⊥PF .
在Rt⊿AOF和Rt⊿EOF中∵AO=EO,OF=OF ∴Rt⊿AOF∽Rt⊿EOF∴∠AOF=∠EOF(5分)
同理∠BOP=∠EOP ∴∠EOF+∠EOP=1/2×180°=90°∴∠EOP=90°即OF⊥OP (7分)
(3)存在(如果这一步不写,但下面各步骤都正确,不扣分) (8分)
∵∠EOF=∠AOF ∴∠EHG=∠AOE=2∠EOF,
∴当∠EHG=∠AOE=2∠EOF,即∠EOF=30°时 Rt⊿EOF∽Rt⊿EHG (10分)
此时∠EOF=30°,∠BOP=∠EOP=90°-30°=60°
∴BP=OB·tan60°=
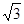 (12分)
(12分)(1)根据切线的性质,将所求四边形CDFP的边转化为已知正方形ABCD的边,即可求得;
(2)连结OE,根据切线的性质和相似三角形,求得∠EOP=90°,即可求得OF⊥OP;
(3)要△EFO∽△EHG,必须∠EHG=∠EFO=2∠EOF=60°,在直角△OBP中,由正切定理可求出BP的长.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
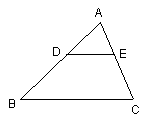
 过圆心
过圆心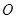 ,交圆
,交圆 两点,
两点,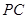 切圆
切圆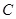 ,作
,作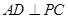 ,垂足为
,垂足为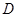 ,连结
,连结 .
.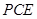 的情形,
的情形,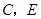 两点,
两点,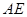 与
与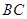 交于点
交于点 ,
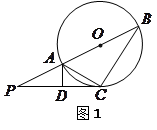
,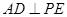 ,写出图2中相等的角(写出三组即可,直角除外);
,写出图2中相等的角(写出三组即可,直角除外);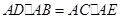 .
.

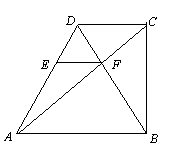
 ,
,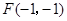 ,以
,以 为位似中心,按比例尺
为位似中心,按比例尺 ,把
,把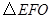 缩小,则点
缩小,则点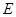 的对应点
的对应点 的坐标为( )
的坐标为( )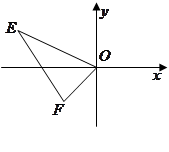
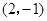 或
或
 或
或

 中,点
中,点 分别在边
分别在边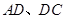 上,
上, ,
,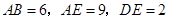 ,求
,求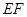 的长.
的长.