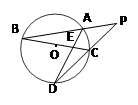题目内容
某市经济开发区建有
 三个食品加工厂,这三个工厂和开发区
三个食品加工厂,这三个工厂和开发区 处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且
处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且 米,
米,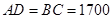 米.自来水公司已经修好一条自来水主管道
米.自来水公司已经修好一条自来水主管道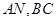 两厂之间的公路与自来水管道交于
两厂之间的公路与自来水管道交于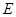 处,
处, 米.若自来水主管道到各工厂的自来水管道由各厂负担,每米造价800元.
米.若自来水主管道到各工厂的自来水管道由各厂负担,每米造价800元.
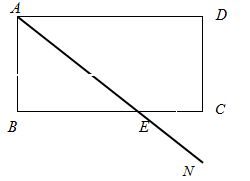
(1)要使修建自来水管道的造价最低,这三个工厂的自来水管道路线应怎样设计?并在图形中画出;
(2)求出各厂所修建的自来水管道的最低的造价各是多少元?

 三个食品加工厂,这三个工厂和开发区
三个食品加工厂,这三个工厂和开发区 处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且
处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且 米,
米,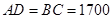 米.自来水公司已经修好一条自来水主管道
米.自来水公司已经修好一条自来水主管道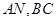 两厂之间的公路与自来水管道交于
两厂之间的公路与自来水管道交于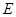 处,
处, 米.若自来水主管道到各工厂的自来水管道由各厂负担,每米造价800元.
米.若自来水主管道到各工厂的自来水管道由各厂负担,每米造价800元.
(1)要使修建自来水管道的造价最低,这三个工厂的自来水管道路线应怎样设计?并在图形中画出;
(2)求出各厂所修建的自来水管道的最低的造价各是多少元?
解:(1)过
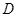 分别作
分别作 的垂线段
的垂线段 ,交
,交 于
于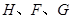 ,
,
 即为所求的造价最低的管道路线.图形如图所示.
即为所求的造价最低的管道路线.图形如图所示.
(2)(法一)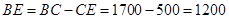 (米),
(米),
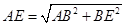 =1500(米),
=1500(米),
∵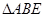 ∽
∽ ,
,
得到: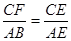 .
.
∴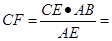
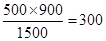 (米).
(米).
∵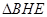 ∽
∽ ,
,
得到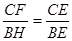 ,
,
∴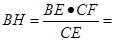
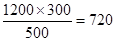 (米),
(米),
∵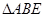 ∽
∽ ,
,
∴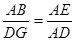 ,
,
∴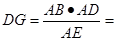
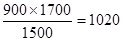 (米),
(米),
所以,
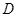 三厂所建自来水管道的最低造价分别是
三厂所建自来水管道的最低造价分别是
720×800=576000(元),300×800=240000(元),1020×800=816000(元)
法二(设 ,利用三角函数可求得
,利用三角函数可求得 的长)
的长)

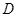 分别作
分别作 的垂线段
的垂线段 ,交
,交 于
于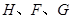 ,
, 即为所求的造价最低的管道路线.图形如图所示.
即为所求的造价最低的管道路线.图形如图所示. (2)(法一)
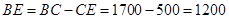 (米),
(米),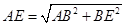 =1500(米),
=1500(米), ∵
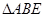 ∽
∽ ,
,得到:
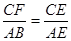 .
.∴
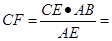
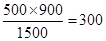 (米).
(米).∵
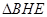 ∽
∽ ,
,得到
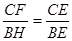 ,
,∴
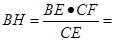
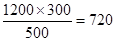 (米),
(米),∵
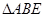 ∽
∽ ,
,∴
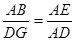 ,
,∴
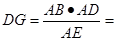
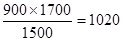 (米),
(米),所以,

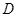 三厂所建自来水管道的最低造价分别是
三厂所建自来水管道的最低造价分别是720×800=576000(元),300×800=240000(元),1020×800=816000(元)
法二(设
 ,利用三角函数可求得
,利用三角函数可求得 的长)
的长)(1)根据“垂线段最短”即可画出使修建自来水管道的造价最低时,这三个工厂的自来水管道路线;
(2)根据勾股定理和直角三角形的面积公式求得BH的长,根据相似三角形的对应边的比相等分别求得CF,DG的长,再根据每米造价800元求得价钱.
(2)根据勾股定理和直角三角形的面积公式求得BH的长,根据相似三角形的对应边的比相等分别求得CF,DG的长,再根据每米造价800元求得价钱.

练习册系列答案
相关题目
 的边长为1,射线
的边长为1,射线 与射线
与射线 交于点
交于点 ,射线
,射线 与射线
与射线 交于点
交于点 ,
, .
.
 、
、 、
、 有怎样的数量关系?并证明你的猜想.
有怎样的数量关系?并证明你的猜想. ,
, ,当点
,当点 、
、 ),如图1,求
),如图1,求 关于
关于 的函数解析式,并指出
的函数解析式,并指出 和以
和以 为半径的
为半径的 之间的位置关系.
之间的位置关系.
 ,如图2.问△
,如图2.问△ 与△
与△ 能否相似,若能相似,求出
能否相似,若能相似,求出
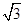 ,则△ADC的面积与△CDB的面积的比为( )
,则△ADC的面积与△CDB的面积的比为( )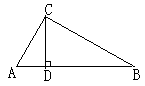
 过圆心
过圆心 ,交圆
,交圆 两点,
两点, 切圆
切圆 ,作
,作 ,垂足为
,垂足为 ,连结
,连结 .
. 的情形,
的情形, 两点,
两点, 与
与 交于点
交于点 ,
, ,写出图2中相等的角(写出三组即可,直角除外);
,写出图2中相等的角(写出三组即可,直角除外); .
.