题目内容
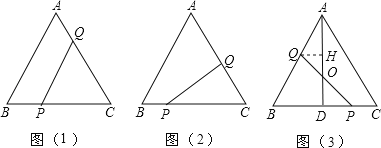
【题目】如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发以每秒1cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上(但不与A点重合),求t的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据中垂线性质可知,作AB的垂直平分线,与AC交于点P,则满足PA=PB,在Rt△ABC中,用勾股定理计算出AC=8cm,再用t表示出PA=t cm,则PC=![]() cm,在Rt△PBC中,利用勾股定理建立方程求t;
cm,在Rt△PBC中,利用勾股定理建立方程求t;
(2)过P作PD⊥AB于D点,由角平分线性质可得PC=PD,由题意PC=![]() cm,则PB=
cm,则PB=![]() cm,在Rt△ABD中,利用勾股定理建立方程求t.
cm,在Rt△ABD中,利用勾股定理建立方程求t.
(1)作AB的垂直平分线交AB于D,交AC于P,连接PB,如图所示,

由垂直平分线的性质可知PA=PB,此时P点满足题意,
在Rt△ABC中,![]() cm,
cm,
由题意PA= t cm,PC=![]() cm,
cm,
在Rt△PBC中,![]() ,
,
即![]() ,解得
,解得![]()
(2)作∠CAB的平分线AP,过P作PD⊥AB于D点,如图所示

∵AP平分∠CAB,PC⊥AC,PD⊥AB,
∴PC=PD
在Rt△ACP和Rt△ADP中,
![]()
∴![]()
∴AD=AC=8cm
∴BD=AB-AD=10-8=2cm
由题意PD=PC=![]() cm,则PB=
cm,则PB=![]() cm,
cm,
在Rt△ABD中,![]()
即![]()
解得![]()

练习册系列答案
相关题目