题目内容
【题目】![]() 与
与![]() 有公共顶点
有公共顶点![]() (顶点均按逆时针排列),
(顶点均按逆时针排列),![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() 并延长交直线
并延长交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
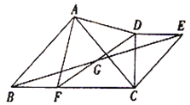
(1)如图,当![]() 时,
时,
求证:①![]() ;
;
②![]() 是等腰直角三角形.
是等腰直角三角形.
(2)当![]() 时,画出相应的图形(画一个即可),并直接指出
时,画出相应的图形(画一个即可),并直接指出![]() 是何种特殊三角形.
是何种特殊三角形.
【答案】(1)①详见解析;②详见解析;(2)详见解析;
【解析】
(1)①由![]() ,
,![]() ,
,![]() 证明三角形全等,得到
证明三角形全等,得到![]() ,即可得到结论;
,即可得到结论;
②由![]() ,则
,则![]() ,然后证明
,然后证明![]() ,得到
,得到![]() ,
,![]() ,然后得到
,然后得到![]() ,即可得到结论成立;
,即可得到结论成立;
(2)根据![]() ,得到△ABC是等边三角形,由(1)可知
,得到△ABC是等边三角形,由(1)可知![]() ,得到
,得到![]() ,
,![]() ,即可判断是等边三角形.
,即可判断是等边三角形.
解:(1)证明:①∵![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() ;
;
②当![]() 时,
时,![]() ,
,
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
又![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
即![]() ,
,
∴![]() 是等腰直角三角形.
是等腰直角三角形.
(2)所画图形如图①或图②,此时![]() 是等边三角形.
是等边三角形.
图①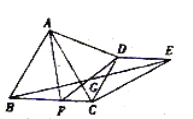
图②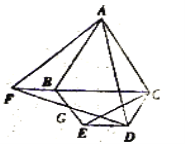
与(1)同理,可证![]() ,
,
∴AF=AD, ![]() ,
,
∴△AFD是等边三角形.

练习册系列答案
相关题目







