题目内容
【题目】如图,正比例函数 ![]() 的图象与反比例函数
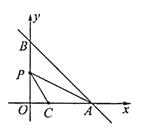
的图象与反比例函数 ![]() 的图象交于A、B两点,点C在x轴负半轴上,AC=AO,△ACO的面积为12.
的图象交于A、B两点,点C在x轴负半轴上,AC=AO,△ACO的面积为12.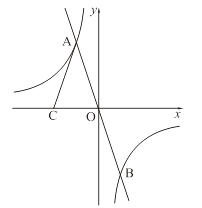
(1)求k的值;
(2)根据图象,当 ![]() 时,写出自变量
时,写出自变量 ![]() 的取值范围.
的取值范围.
【答案】
(1)
解:如图,过点A作AD⊥OC于点D.
又∵AC=AO.
∴CD=DO.
∴S△ADO=![]() S△ACO=6.
S△ACO=6.
∴k=-12.
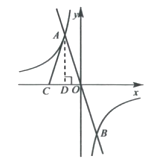
(2)
解:由图像可知:χ<-2或0<χ<2.
【解析】(1)如图,过点A作AD⊥OC于点D,根据等腰三角形的性质可以得出S△ADO=![]() S△ACO=6;从而求出k的值.
S△ACO=6;从而求出k的值.
(2)从图像可以得出答案.
【考点精析】解答此题的关键在于理解反比例函数的性质的相关知识,掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大,以及对比例系数k的几何意义的理解,了解几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目