题目内容
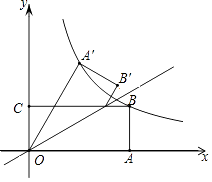
【题目】如图,在平面直角坐标系xOy中,直线y=-x+m分别交于x轴、y轴于A,B两点,已知点C(2,0).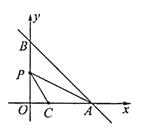
(1)当直线AB经过点C时,点O到直线AB的距离是;
(2)设点P为线段OB的中点,连结PA,PC,若∠CPA=∠ABO,则m的值是.
【答案】
(1)![]()
(2)12
【解析】解:(1)当直线AB经过点C时,点A与点C重合,
当x=2时,y=-2+m=0,即m=2.
∴直线AB为y=-x+2,则B(0,2)
∴OB=OA=2,AB=2 ![]() ,
,
设点O到直线AB的距离是d,
由S△OAB= ![]() ,
,
则4=2 ![]() d,
d,
∴d= ![]() .
.
2)作OD=OC=2,则∠PDC=45°,如图,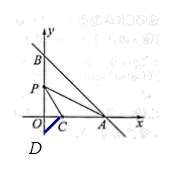
由y=-x+m可得A(m,0),B(0,m),
则可得OA=OB,则∠OBA=∠OAB=45°,
当m<0时,∠APO>∠OBA=45°,∴此时∠CPA>45°,故不符合,
∴m>0.
∵∠CPA=∠ABO=45°,
∴∠BPA+∠OPC=∠BAP+∠BPA=135°,
即∠OPC=∠BAP,
则△PCD~△APB,
∴ ![]() ,
,
即 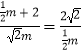 ,
,
解得m=12.
所以答案是 ![]() ;12.
;12.
【考点精析】根据题目的已知条件,利用一次函数的性质和相似三角形的应用的相关知识可以得到问题的答案,需要掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.

练习册系列答案
相关题目