Question

【题目】已知：如图，抛物线y=ax2﹣2ax+c（a≠0）与y轴交于点C（0，4），与x轴交于点A、B，点A的坐标为（4，0）．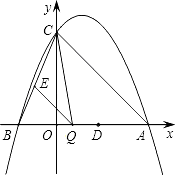

（1）求该抛物线的解析式；
（2）点Q是线段AB上的动点，过点Q作QE∥AC，交BC于点E，连接CQ．当△CQE的面积最大时，求点Q的坐标；
（3）若平行于x轴的动直线l与该抛物线交于点P，与直线AC交于点F，点D的坐标为（2，0）．问：是否存在这样的直线l，使得△ODF是等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：由题意，得

解得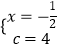

∴所求抛物线的解析式为：y=﹣ x2+x+4

（2）

解：设点Q的坐标为（m，0），过点E作EG⊥x轴于点G．

由﹣ x2+x+4=0，

得x1=﹣2，x2=4

∴点B的坐标为（﹣2，0）

∴AB=6，BQ=m+2

∵QE∥AC

∴△BQE∽△BAC

∴

即

∴

∴S△CQE=S△CBQ﹣S△EBQ

= BQCO﹣ BQEG

= （m+2）（4﹣ ）

=

=﹣ （m﹣1）2+3

又∵﹣2≤m≤4

∴当m=1时，S△CQE有最大值3，此时Q（1，0）

（3）

解：存在．在△ODF中．

（ⅰ）若DO=DF

∵A（4，0），D（2，0）

∴AD=OD=DF=2

又在Rt△AOC中，OA=OC=4

∴∠OAC=45度

∴∠DFA=∠OAC=45度

∴∠ADF=90度．此时，点F的坐标为（2，2）

由﹣ x2+x+4=2，

得x1=1+ ，x2=1﹣

此时，点P的坐标为：P（1+ ，2）或P（1﹣ ，2）．

（ⅱ）若FO=FD，过点F作FM⊥x轴于点M

由等腰三角形的性质得：OM= OD=1

∴AM=3

∴在等腰直角△AMF中，MF=AM=3

∴F（1，3）

由﹣ x2+x+4=3，

得x1=1+ ，x2=1﹣

此时，点P的坐标为：P（1+ ，3）或P（1﹣ ，3）．

（ⅲ）若OD=OF

∵OA=OC=4，且∠AOC=90°

∴AC=

∴点O到AC的距离为 ，而OF=OD=2 ，与OF≥2 矛盾，所以AC上不存在点使得OF=OD=2，

此时，不存在这样的直线l，使得△ODF是等腰三角形

综上所述，存在这样的直线l，使得△ODF是等腰三角形

所求点P的坐标为：P（1+ ，2）或P（1﹣ ，2）或P（1+ ，3）或P（1﹣ ，3）．

【解析】（1）根据抛物线过C（0，4）点，可确定c=4，然后可将A的坐标代入抛物线的解析式中，即可得出二次函数的解析式．（2）可先设Q的坐标为（m，0）；通过求△CEQ的面积与m之间的函数关系式，来得出△CQE的面积最大时点Q的坐标．△CEQ的面积=△CBQ的面积﹣△BQE的面积．可用m表示出BQ的长，然后通过相似△BEQ和△BCA得出△BEQ中BQ边上的高，进而可根据△CEQ的面积计算方法得出△CEQ的面积与m的函数关系式，可根据函数的性质求出△CEQ的面积最大时，m的取值，也就求出了Q的坐标．（3）本题要分三种情况进行求解：①当OD=OF时，OD=DF=AD=2，又有∠OAF=45°，那么△OFA是个等腰直角三角形，于是可得出F的坐标应该是（2，2）．由于P，F两点的纵坐标相同，因此可将F的纵坐标代入抛物线的解析式中即可求出P的坐标．②当OF=DF时，如果过F作FM⊥OD于M，那么FM垂直平分OD，因此OM=1，在直角三角形FMA中，由于∠OAF=45°，因此FM=AM=3，也就得出了F的纵坐标，然后根据①的方法求出P的坐标．③当OD=OF时，OF=2，由于O到AC的最短距离为2 ，因此此种情况是不成立的．综合上面的情况即可得出符合条件的P的坐标．