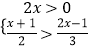Question

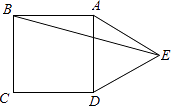
【题目】已知：如图，MN为⊙O的直径，ME是⊙O的弦，MD垂直于过点E的直线DE，垂足为点D，且ME平分∠DMN．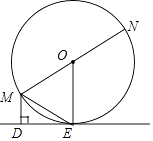
求证：
（1）DE是⊙O的切线；
（2）ME2=MDMN．

Answer 1

【答案】
（1）证明：∵ME平分∠DMN，

∴∠OME=∠DME，

∵OM=OE，

∴∠OME=∠OEM，

∴∠DME=∠OEM，

∴OE∥DM，

∵DM⊥DE，

∴OE⊥DE，

∵OE过O，

∴DE是⊙O的切线；

（2）证明：连接EN，

∵DM⊥DE，MN为⊙O的半径，

∴∠MDE=∠MEN=90°，

∵∠NME=∠DME，

∴△MDE∽△MEN，

∴ = ，

∴ME2=MDMN

【解析】（1）求出OE∥DM，求出OE⊥DE，根据切线的判定得出即可；（2）连接EN，求出∠MDE=∠MEN，求出△MDE∽△MEN，根据相似三角形的判定得出即可．
【考点精析】根据题目的已知条件，利用相似三角形的判定与性质的相关知识可以得到问题的答案，需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．