题目内容
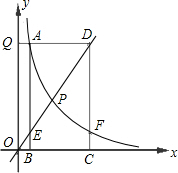
已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=
(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:
①双曲线的解析式为y=
(x>0);
②E点的坐标是(4,8);
③sin∠COA=
;
④AC+OB=12
,其中正确的结论有( )

| k |
| x |
①双曲线的解析式为y=
| 20 |
| x |
②E点的坐标是(4,8);
③sin∠COA=
| 4 |
| 5 |
④AC+OB=12
| 5 |
| A.1个 | B.2个 | C.3个 | D.4个 |

过点C作CF⊥x轴于点F,
∵OB•AC=160,A点的坐标为(10,0),
∴OA•CF=
OB•AC=
×160=80,菱形OABC的边长为10,
∴CF=
=
=8,
在Rt△OCF中,
∵OC=10,CF=8,
∴OF=
=
=6,
∴C(6,8),
∵点D时线段AC的中点,
∴D点坐标为(
,
),即(8,4),
∵双曲线y=
(x>0)经过D点,
∴4=
,即k=32,
∴双曲线的解析式为:y=
(x>0),故①错误;
∵CF=8,
∴直线CB的解析式为y=8,
∴
,解得
,
∴E点坐标为(4,8),故②正确;
∵CF=8,OC=10,
∴sin∠COA=
=
=
,故③正确;
∵A(10,0),C(6,8),
∴AC=
=4
,
∵OB•AC=160,
∴OB=
=
=8
,
∴AC+OB=4
+8
=12
,故④正确.
故选C.
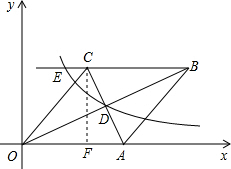
∵OB•AC=160,A点的坐标为(10,0),
∴OA•CF=
| 1 |
| 2 |
| 1 |
| 2 |
∴CF=
| 80 |
| OA |
| 80 |
| 10 |
在Rt△OCF中,
∵OC=10,CF=8,
∴OF=
| OC2-CF2 |
| 102-82 |
∴C(6,8),
∵点D时线段AC的中点,
∴D点坐标为(
| 10+6 |
| 2 |
| 8 |
| 2 |
∵双曲线y=
| k |
| x |
∴4=
| k |
| 8 |
∴双曲线的解析式为:y=
| 32 |
| x |
∵CF=8,
∴直线CB的解析式为y=8,
∴
|
|
∴E点坐标为(4,8),故②正确;
∵CF=8,OC=10,
∴sin∠COA=
| CF |
| OC |
| 8 |
| 10 |
| 4 |
| 5 |
∵A(10,0),C(6,8),
∴AC=
| (10-6)2+(0-8)2 |
| 5 |
∵OB•AC=160,
∴OB=
| 160 |
| AC |
| 160 | ||
4
|
| 5 |
∴AC+OB=4
| 5 |
| 5 |
| 5 |
故选C.


练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
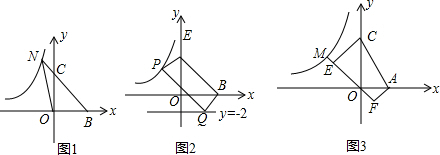
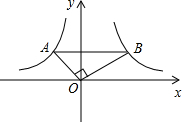
 图象相交于A、B两点.
图象相交于A、B两点.