题目内容
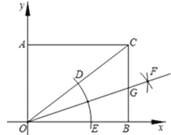
【题目】如图，已知矩形 AOBC 的三个顶点的坐标分别为 O(0，0)，A(0，3)， B(4，0)，按以下步骤作图：①以点 O 为圆心，适当长度为半径作弧， 分别交 OC，OB 于点 D，E；②分别以点 D，E 为圆心，大于 
DE 的长为半径作弧，两弧在∠BOC 内交于点 F；③作射线 OF，交边 BC于点 G，则点 G 的坐标为( )
A. (4， 
)B. ( ，4)C. ( 
，4)D. (4， )
【答案】A
【解析】
首作GH⊥OC于H．先证明GB=GH，利用面积法求出GB即可解决问题．
解：∵四边形AOBC是矩形，A（0，3），B（4，0），
∴OB＝4，OA＝BC＝3，∠OBC＝90°，
∴BC＝
＝5，
作GH⊥OC于H．
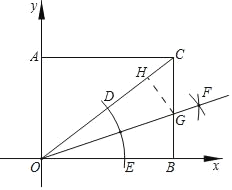
由作图可知：OG平分∠BOC，
∵GB⊥OB，GH⊥OC，
∴GB＝GH时，GB＝GH＝x，
∵S△OBC＝
×3×4＝×5×x+×4×x，
∴x＝
，
∴G（4，）．
故选：A．
练习册系列答案
相关题目
