题目内容
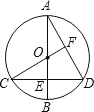
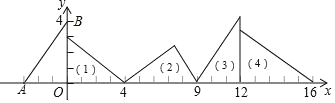
【题目】如图,在直角坐标系中,已知点 A(﹣3,0),B(0,4),对△OAB 连续作旋转变换,依次得到三角形(1),(2),(3),(4)…,则三角形(2019)的直角顶点的坐标为_____.
【答案】(8076,0)
【解析】
先利用勾股定理计算出AB,从而得到△ABC的周长为12,根据旋转变换可得△OAB的旋转变换为每3次一个循环,由于2019=3×673,于是可判断三角形2019与三角形1的状态一样,然后计算673×12即可得到三角形2019的直角顶点坐标.
解:∵A(-3,0),B(0,4),
∴OA=3,OB=4,
∴AB=![]() =5,
=5,
∴△ABC的周长=3+4+5=12,
∵△OAB每连续3次后与原来的状态一样,
∵2019=3×673,
∴三角形2019与三角形1的状态一样,
∴三角形2019的直角顶点的横坐标=673×12=8076,
∴三角形2019的直角顶点坐标为(8076,0).
故答案为(8076,0).

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目