题目内容
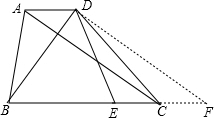
如图，梯形ABCD中，AD∥BC，AC⊥BD，AD=3，BC=7，E在BC上，CE=2，则DE=______．
过D作DF∥AC交BC的延长线于F，
∵AD∥BC，
∴四边形ACFD是平行四边形，
∴CF=AD=3，
∵BC=7，
∴BF=BC+CF=7+3=10，
∵CE=2，
∴BE=7-2=5，EF=2+3=5，
∴BE=EF，
又∵AC⊥BD，DF∥AC，
∴∠BDC=90°，
∴DE=
BF=5．
∵AD∥BC，
∴四边形ACFD是平行四边形，
∴CF=AD=3，
∵BC=7，
∴BF=BC+CF=7+3=10，
∵CE=2，
∴BE=7-2=5，EF=2+3=5，
∴BE=EF，
又∵AC⊥BD，DF∥AC，
∴∠BDC=90°，
∴DE=
| 1 |
| 2 |
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
