题目内容
如图,已知在平行四边形ABED中,AE是对角线,∠B=∠EAD,延长BE至点C,使EC=BE,并连接DC.
(1)求证:四边形ABCD是等腰梯形;
(2)若AB=AD=4,求梯形ABCD的面积.

(1)求证:四边形ABCD是等腰梯形;
(2)若AB=AD=4,求梯形ABCD的面积.

证明:(1)∵四边形ABED是平行四边形,
∴AD=BE,AD∥BE,
∴∠EAD=∠AEB,
∵∠B=∠EAD,
∴∠AEB=∠B,
∴AB=AE,
∵EC=BE,AD=BE,
∴AD=EC,
∵AD∥BE,
∴AD∥EC,
∴四边形AECD是平行四边形,
∴AE=CD,
∵AE=AB,
∴AB=CD,
∵AD∥BC,
∴四边形ABCD是等腰梯形;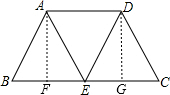
(2)∵AB=AD=4,AB=EC.AB=DC,
∴DC=4,=AB,BC=8,
过A作AF⊥BC于F,过D作DG⊥BC于G,
则∠AFB=∠AFE=∠DGC=90°,AF∥DG,
∵AD∥BC,
∴四边形AFGD是矩形,
∴AD=GF=4,AF=DG,
∵AB=CD,
∴由勾股定理得:BF=CG=2,
由勾股定理得:AF=
=2
,
∴梯形ABCD的面积是
×(4+8)×4=24.
∴AD=BE,AD∥BE,
∴∠EAD=∠AEB,
∵∠B=∠EAD,
∴∠AEB=∠B,
∴AB=AE,
∵EC=BE,AD=BE,
∴AD=EC,
∵AD∥BE,
∴AD∥EC,
∴四边形AECD是平行四边形,
∴AE=CD,
∵AE=AB,
∴AB=CD,
∵AD∥BC,
∴四边形ABCD是等腰梯形;

(2)∵AB=AD=4,AB=EC.AB=DC,
∴DC=4,=AB,BC=8,
过A作AF⊥BC于F,过D作DG⊥BC于G,
则∠AFB=∠AFE=∠DGC=90°,AF∥DG,
∵AD∥BC,
∴四边形AFGD是矩形,
∴AD=GF=4,AF=DG,
∵AB=CD,
∴由勾股定理得:BF=CG=2,
由勾股定理得:AF=
| 42-22 |
| 3 |
∴梯形ABCD的面积是
| 1 |
| 2 |

练习册系列答案
相关题目







