题目内容
【题目】如图,在长方形![]() 中,
中,![]() 为平面直角坐标系的原点,点
为平面直角坐标系的原点,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,点
轴上,点![]() 在第一象限内,点
在第一象限内,点![]() 从原点出发,以每秒
从原点出发,以每秒![]() 个单位长度的速度沿着
个单位长度的速度沿着![]() 的路线移动(即沿着长方形的边移动一周).
的路线移动(即沿着长方形的边移动一周).
(1)分别求出![]() ,
,![]() 两点的坐标;
两点的坐标;
(2)当点![]() 移动了
移动了![]() 秒时,求出点
秒时,求出点![]() 的坐标;
的坐标;
(3)在移动过程中,当三角形![]() 的面积是
的面积是![]() 时,求满足条件的点
时,求满足条件的点![]() 的坐标及相应的点
的坐标及相应的点![]() 移动的时间.
移动的时间.
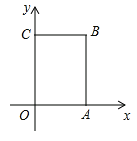
【答案】(1)点![]() ,点
,点![]() ;(2)点
;(2)点![]() ;(3)①P(0,5),移动时间为
;(3)①P(0,5),移动时间为![]() 秒;②P(
秒;②P(![]() ,6),移动时间为
,6),移动时间为![]() 秒;③P(4,1),移动时间为:
秒;③P(4,1),移动时间为:![]() 秒;④P(
秒;④P(![]() ,0),移动时间为:
,0),移动时间为:![]() 秒
秒
【解析】
(1)根据点A,点C的位置即可解答;
(2)根据点P的速度及移动时间即可解答;
(3)对点P的位置分类讨论,根据三角形的面积计算公式即可解答.
解:(1)点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,
轴上,
∴m+2=0,n-1=0,
∴m=-2,n=1.
∴点![]() ,点
,点![]()
(2)由(1)可知:点![]() ,点
,点![]()
当点![]() 移动了
移动了![]() 秒时,移动的路程为:4×2=8,
秒时,移动的路程为:4×2=8,
∴此时点P在CB上,且CP=2,
∴点![]() .
.
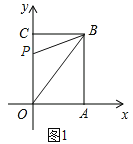
(3)①如图1所示,当点P在OC上时,
∵△OBP的面积为10,
∴![]() ,即
,即![]() ,解得OP=5,
,解得OP=5,
∴点P的坐标为(0,5),运动时间为:![]() (秒)
(秒)
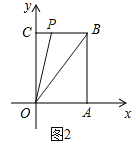
②如图2所示,当点P在BC上时,
∵△OBP的面积为10,
∴![]() ,即
,即![]() ,解得BP=
,解得BP=![]() ,
,
∴CP=![]()
∴点P的坐标为(![]() ,6),运动时间为:
,6),运动时间为:![]() (秒)
(秒)
③如图3所示,当点P在AB上时,
∵△OBP的面积为10,
∴![]() ,即
,即![]() ,解得BP=5,
,解得BP=5,
∴AP=1
∴点P的坐标为(4,1),运动时间为:![]() (秒)
(秒)

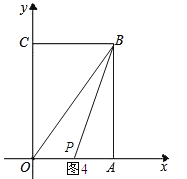
④如图4所示,当点P在OA上时,
∵△OBP的面积为10,
∴![]() ,即
,即![]() ,解得OP=
,解得OP=![]() ,
,
∴点P的坐标为(![]() ,0),运动时间为:
,0),运动时间为:![]() (秒)
(秒)
综上所述:①P(0,5),移动时间为![]() 秒;②P(
秒;②P(![]() ,6),移动时间为
,6),移动时间为![]() 秒;③P(4,1),移动时间为:
秒;③P(4,1),移动时间为:![]() 秒;④P(
秒;④P(![]() ,0),移动时间为:
,0),移动时间为:![]() 秒.
秒.

练习册系列答案
相关题目