题目内容
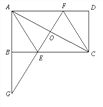
【题目】如图,在平行四边形ABCD中,点O是AC中点,AC=2AB,延长AB到G,使BG=AB,连接GO并延长,分别交BC于点E,交AD于点F.
(1)求证:△ABC≌△AOG;
(2)若ABCD为矩形,则四边形AECF是什么特殊四边形?请说明理由.
【答案】(1)见解析;(2)见解析.
【解析】(1)由O是AC的中点,AC=2AB,BG=AB,得到AO=AB,AC=AG.由∠BAC=∠OAG ,即可得到结论;
(2)由O是AC的中点,得到AO=OC.由平行四边形的性质得到AF∥EC,由平行线的性质得到∠DAO=∠BCO,进而得到△AOF≌△COE, AF=CE,得到四边形AECF是平行四边形.由△ABC≌△AOG,得到∠AOG=∠ABC=90°,即可得到AECF是菱形.
(1)∵O是AC的中点,AC=2AB,BG=AB,∴AO=AB,AC=AG.
又∵∠BAC=∠OAG ,∴△ABC≌△AOG;
(2)AECF是菱形.理由如下:
∵O是AC的中点,∴AO=OC.
∵平行四边形ABCD,∴AF∥EC,∴∠DAO=∠BCO.
又∵∠AOF=∠COE,∴△AOF≌△COE,∴AF=CE,∴四边形AECF是平行四边形.
由(1)知△ABC≌△AOG,∴∠AOG=∠ABC.
又∵ABCD是矩形,
∴∠ABC=90°,∴∠AOG=90°,∴AECF是菱形.

练习册系列答案
相关题目