题目内容
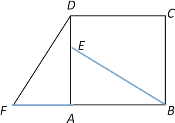
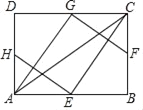
【题目】如图,E、F、G、H分别为矩形ABCD的边AB、BC、CD、DA的中点,连接AC、HE、EC,GA,GF.已知AG⊥GF,AC=![]() ,则AB的长为__________.
,则AB的长为__________.
【答案】2
【解析】连接BD.由△ADG∽△GCF,设CF=BF=a,CG=DG=b,可得![]() ,推出
,推出![]() ,可得b=
,可得b=![]() a,在Rt△GCF中,利用勾股定理求出b,即可解决问题;
a,在Rt△GCF中,利用勾股定理求出b,即可解决问题;
如图,连接BD.

∵四边形ABCD是矩形,
∴∠ADC=∠DCB=90°,AC=BD=![]() ,
,
∵CG=DG,CF=FB,
∴GF=![]() BD=
BD=![]() ,
,
∵AG⊥FG,
∴∠AGF=90°,
∴∠DAG+∠AGD=90°,∠AGD+∠CGF=90°,
∴∠DAG=∠CGF,
∴△ADG∽△GCF,设CF=BF=a,CG=DG=b,
∴![]() ,
,
∴![]() ,
,
∴b2=2a2,
∵a>0.b>0,
∴b=![]() a,
a,
在Rt△GCF中,3a2=![]() ,
,
∴a=![]() ,
,
∴AB=2b=2.
故答案为2.

练习册系列答案
相关题目