题目内容
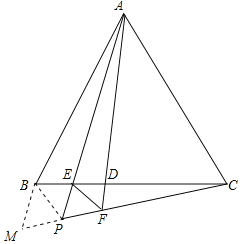
【题目】如图，在△ABC中，点D为线段BC上一点（不含端点），AP平分∠BAD交BC于E，PC与AD的延长线交于点F，连接EF，且∠PEF＝∠AED．
（1）求证：AB＝AF；
（2）若△ABC是等边三角形．
①求∠APC的大小；
②想线AP，PF，PC之间满足怎样的数量关系，并证明．
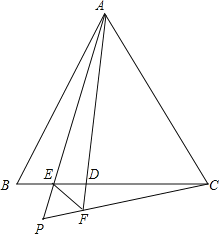
【答案】（1）详见解析；（2）①60°；②AP＝PF+PC，理由详见解析．
【解析】
（1）由已知证出∠AEB＝∠AEF，∠BAP＝∠FAP，证明△AEB≌△AEF，即可得出AB＝AF；
（2）①由等边三角形的性质得出AB＝AC＝BC，∠BAC＝60°，证出AF＝AC，设∠BAP＝∠FAP＝x，则∠FAC＝60°﹣2x，求出∠AFC＝x+60°，由三角形的外角性质得出∠AFC＝∠FAP+∠APC＝x+∠APC，即可得出结果；
②延长CP至点M，使PM＝PF，连接BM、BP，先证明△APB≌△APF，得出∠APC＝∠APB＝60°，PB＝PF，得出∠BPM＝60°，PM＝PB，得出△BPM是等边三角形，得出BP＝BM，∠ABP＝∠CBM＝60°+∠PBC，再证明△ABP≌△CBM，即可得出结论．
（1）证明：∵∠PEF＝∠AED，
∴180°﹣∠PEF＝180°﹣∠AED，
∴∠AEB＝∠AEF，
∵AP平分∠BAD，
∴∠BAP＝∠FAP，
在△AEB和△AEF中，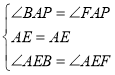
，
∴△AEB≌△AEF（ASA），
∴AB＝AF；
（2）解：①∵△ABC是等边三角形，
∴AB＝AC＝BC，∠BAC＝60°，
∵AB＝AF，
∴AF＝AC，
设∠BAP＝∠FAP＝x，则∠FAC＝60°﹣2x，
在△ACF中，∠AFC＝
[180°﹣（60°﹣2x）]＝x+60°，
又∵∠AFC＝∠FAP+∠APC＝x+∠APC，
∴∠APC＝60°；
②AP＝PF+PC，理由如下：
延长CP至点M，使PM＝PF，连接BM、BP，如图所示：
在△APB和△APF中，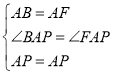
，
∴△APB≌△APF（SAS），
∴∠APC＝∠APB＝60°，PB＝PF，
∴∠BPM＝60°，PM＝PB，
∴△BPM是等边三角形，
∴BP＝BM，∠ABP＝∠CBM＝60°+∠PBC，
在△ABP和△CBM中，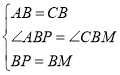
，
∴△ABP≌△CBM（SAS），
∴AP＝CM＝PM+PC＝PF+PC．
