جâؤ؟ؤعبف
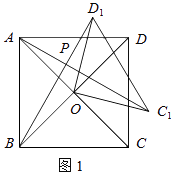
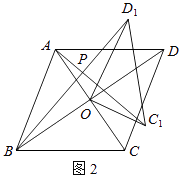
،¾جâؤ؟،؟شعثؤ±كذخABCDضذ£¬¶ش½ادكAC،¢BDدཻسعµمO£¬½«،÷CODبئµمO°´ؤوت±صë·½دٍذ×ھµأµ½،÷C1OD1 £¬ ذ×ھ½اخھ¦ب£¨0،م£¼¦ب£¼90،م£©£¬ء¬½سAC1،¢BD1 £¬ AC1سëBD1½»سعµمP£®
£¨1£©بçح¼1£¬بôثؤ±كذخABCDتاص·½ذخ£®
¢ظاَض¤£؛،÷AOC1،ص،÷BOD1 £®
¢عاëض±½سذ´³ِAC1 سëBD1µؤخ»ضأ¹طدµ£®
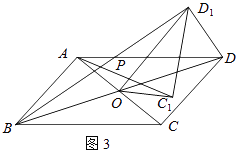
£¨2£©بçح¼2£¬بôثؤ±كذخABCDتاءâذخ£¬AC=5£¬BD=7£¬ةèAC1=kBD1 £® إذ¶دAC1سëBD1µؤخ»ضأ¹طدµ£¬ثµأ÷ہيسة£¬²¢اَ³ِkµؤضµ£®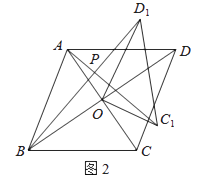
£¨3£©بçح¼3£¬بôثؤ±كذخABCDتائ½ذذثؤ±كذخ£¬AC=5£¬BD=10£¬ء¬½سDD1 £¬ ةèAC1=kBD1 £® اëض±½سذ´³ِkµؤضµ؛حAC12+£¨kDD1£©2µؤضµ£®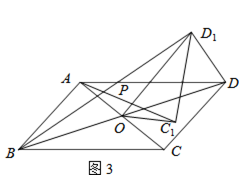
،¾´ً°¸،؟
£¨1£©
¢ظض¤أ÷£؛بçح¼1£¬
،كثؤ±كذخABCDتاص·½ذخ£¬
،àOC=OA=OD=OB£¬AC،حBD£¬
،à،دAOB=،دCOD=90،م£¬
،ك،÷CODبئµمO°´ؤوت±صë·½دٍذ×ھµأµ½،÷C1OD1£¬
،àOC1=OC£¬OD1=OD£¬،دCOC1=،دDOD1£¬
،àOC1=OD1£¬،دAOC1=،دBOD1=90،م+،دAOD1£¬
شع،÷AOC1؛ح،÷BOD1ضذ
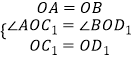 £¬
£¬
،à،÷AOC1،ص،÷BOD1£¨SAS£©£»
¢عAC1،حBD1£»
£¨2£©
½â£؛AC1،حBD1£®
ہيسةبçدآ£؛بçح¼2£¬
،كثؤ±كذخABCDتاءâذخ£¬
،àOC=OA= ![]() AC£¬OD=OB=
AC£¬OD=OB= ![]() BD£¬AC،حBD£¬
BD£¬AC،حBD£¬
،à،دAOB=،دCOD=90،م£¬
،ك،÷CODبئµمO°´ؤوت±صë·½دٍذ×ھµأµ½،÷C1OD1£¬
،àOC1=OC£¬OD1=OD£¬،دCOC1=،دDOD1£¬
،àOC1=OA£¬OD1=OB£¬،دAOC1=،دBOD1£¬
،à ![]() £¬
£¬
،à،÷AOC1،×،÷BOD1£¬
،à،دOAC1=،دOBD1£¬
سض،ك،دAOB=90،م£¬
،à،دOAB+،دABP+،دOBD1=90،م£¬
،à،دOAB+،دABP+،دOAC1=90،م£¬
،à،دAPB=90،م
،àAC1،حBD1£»
،ك،÷AOC1،×،÷BOD1£¬
،à ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() £¬
£¬
،àk= ![]() £»
£»
£¨3£©
½â£؛بçح¼3£¬س루2£©ز»رù؟ةض¤أ÷،÷AOC1،×،÷BOD1£¬
،à ![]() =
= ![]() =
= ![]() =
= ![]() £¬
£¬
،àk= ![]() £»
£»
،ك،÷CODبئµمO°´ؤوت±صë·½دٍذ×ھµأµ½،÷C1OD1£¬
،àOD1=OD£¬
¶ّOD=OB£¬
،àOD1=OB=OD£¬
،à،÷BDD1خھض±½اب½اذخ£¬
شعRt،÷BDD1ضذ£¬
BD12+DD12=BD2=100£¬
،ࣨ2AC1£©2+DD12=100£¬
،àAC12+£¨kDD1£©2=25£®
،¾½âخِ،؟£¨1£©¢ظبçح¼1£¬¸ù¾فص·½ذخµؤذشضتµأOC=OA=OD=OB£¬AC،حBD£¬شٍ،دAOB=،دCOD=90،م£¬شظ¸ù¾فذ×ھµؤذشضتµأOC1=OC£¬OD1=OD£¬،دCOC1=،دDOD1 £¬ شٍOC1=OD1 £¬ ہûسأµب½اµؤ²¹½ادàµبµأ،دAOC1=،دBOD1 £¬ ب»؛َ¸ù¾ف،°SAS،±؟ةض¤أ÷،÷AOC1،ص،÷BOD1£»¢عسة،دAOB=90،م£¬شٍ،دOAB+،دABP+،دOBD1=90،م£¬ثùزش،دOAB+،دABP+،دOAC1=90،م£¬شٍ،دAPB=90،مثùزشAC1،حBD1£»£¨2£©بçح¼2£¬¸ù¾فءâذخµؤذشضتµأOC=OA= ![]() AC£¬OD=OB=
AC£¬OD=OB= ![]() BD£¬AC،حBD£¬شٍ،دAOB=،دCOD=90،م£¬شظ¸ù¾فذ×ھµؤذشضتµأOC1=OC£¬OD1=OD£¬،دCOC1=،دDOD1 £¬ شٍOC1=OA£¬OD1=OB£¬ہûسأµب½اµؤ²¹½ادàµبµأ،دAOC1=،دBOD1 £¬ ¼سةد
BD£¬AC،حBD£¬شٍ،دAOB=،دCOD=90،م£¬شظ¸ù¾فذ×ھµؤذشضتµأOC1=OC£¬OD1=OD£¬،دCOC1=،دDOD1 £¬ شٍOC1=OA£¬OD1=OB£¬ہûسأµب½اµؤ²¹½ادàµبµأ،دAOC1=،دBOD1 £¬ ¼سةد ![]() £¬¸ù¾فدàثئب½اذخµؤإذ¶¨·½·¨µأµ½،÷AOC1،×،÷BOD1 £¬ µأµ½،دOAC1=،دOBD1 £¬ سة،دAOB=90،مµأ،دOAB+،دABP+،دOBD1=90،م£¬شٍ،دOAB+،دABP+،دOAC1=90،م£¬شٍ،دAPB=90،م£¬ثùزشAC1،حBD1£»ب»؛َ¸ù¾فدàثئ±بµأµ½
£¬¸ù¾فدàثئب½اذخµؤإذ¶¨·½·¨µأµ½،÷AOC1،×،÷BOD1 £¬ µأµ½،دOAC1=،دOBD1 £¬ سة،دAOB=90،مµأ،دOAB+،دABP+،دOBD1=90،م£¬شٍ،دOAB+،دABP+،دOAC1=90،م£¬شٍ،دAPB=90،م£¬ثùزشAC1،حBD1£»ب»؛َ¸ù¾فدàثئ±بµأµ½ ![]() =
= ![]() =
= ![]() =
= ![]() £¬ثùزشk=
£¬ثùزشk= ![]() £»£¨3£©س루2£©ز»رù؟ةض¤أ÷،÷AOC1،×،÷BOD1 £¬ شٍ
£»£¨3£©س루2£©ز»رù؟ةض¤أ÷،÷AOC1،×،÷BOD1 £¬ شٍ ![]() =
= ![]() =
= ![]() =
= ![]() £¬ثùزشk=
£¬ثùزشk= ![]() £»¸ù¾فذ×ھµؤذشضتµأOD1=OD£¬¸ù¾فئ½ذذثؤ±كذخµؤذشضتµأOD=OB£¬شٍOD1=OB=OD£¬سعتا؟ةإذ¶د،÷BDD1خھض±½اب½اذخ£¬¸ù¾ف¹´¹ة¶¨ہيµأBD12+DD12=BD2=100£¬ثùزش£¨2AC1£©2+DD12=100£¬سعتاسذAC12+£¨kDD1£©2=25£®
£»¸ù¾فذ×ھµؤذشضتµأOD1=OD£¬¸ù¾فئ½ذذثؤ±كذخµؤذشضتµأOD=OB£¬شٍOD1=OB=OD£¬سعتا؟ةإذ¶د،÷BDD1خھض±½اب½اذخ£¬¸ù¾ف¹´¹ة¶¨ہيµأBD12+DD12=BD2=100£¬ثùزش£¨2AC1£©2+DD12=100£¬سعتاسذAC12+£¨kDD1£©2=25£®

 أ¢¹û½ج¸¨´ï±ê²âتش¾يدµءذ´ً°¸
أ¢¹û½ج¸¨´ï±ê²âتش¾يدµءذ´ً°¸