��Ŀ����
����Ŀ��ͬѧ�ǣ��ڳ�һѧϰ������κ�Բ��ڿ�ʱ�����Ǿ�ѧϰ���ı��ε��ڽǺ͵���360�����������Ǿ����ı��������о��������⣺
(1)���ⱳ����
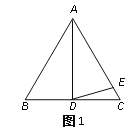
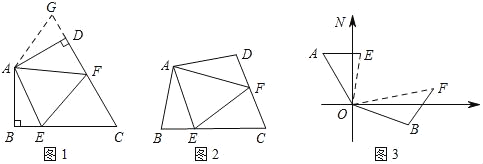
��ͼ1�����ı���ABCD�У�AB��AD����BAD��120������B����ADC��90����E��F�ֱ���BC��CD�ϵĵ㣬�ҡ�EAF��60����̽��ͼ���߶�BE��EF��FD֮���������ϵ��
С��ͬѧ̽��������ķ����ǣ��ӳ�FD����G��ʹDG��BE������AG����֤����ABE�ա�ADG����֤����AEF�ա�AGF���ɵó����ۣ����Ľ���Ӧ��______��
(2)̽�����죺
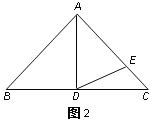
��ͼ2�������ı���ABCD�У�AB��AD����B+��D��180����E��F�ֱ���BC��CD�ϵĵ㣬�ҡ�EAF��![]() ��BAD�����������Ƿ��Գ�������˵�����ɣ�
��BAD�����������Ƿ��Գ�������˵�����ɣ�
(3)ʵ��Ӧ�ã�
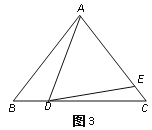
��ͼ3����ij�ξ�����ϰ�У���ͧ����ָ������(��O��)��ƫ��30����A������ͧ����ָ��������ƫ��70����B������������ͧ��ָ�����ĵľ�����ȣ��ӵ��ж�ָ���ͧ��������������45����/ʱ���ٶ�ǰ����ͬʱ����ͧ���ر�ƫ��50���ķ�����60����/ʱ���ٶ�ǰ����2Сʱ��ָ�����Ĺ۲쵽�ס�������ͧ�ֱ�E��F����������֮ͧ��ļн�Ϊ70���������ʱ����֮ͧ��ľ��룮
���𰸡�(1)EF��BE+DF��(2)����EF��BE+DF��Ȼ������(3)��ʱ����֮ͧ��ľ�����210���
��������
(1)�ӳ�FD����G.ʹDG=BE.����AG,����֤����ABE�ա�ADG,�ɵ�AE=AG,��֤����AEF�ա�AGF,�ɵ�EF=FG,���ɽ���;
(2)�ӳ�FD����G.ʹDG=BE.����AG,����֤����ABE�ա�ADG,�ɵ�AE=AG,��֤����AEF�ա�AGF,�ɵ�EF=FG,���ɽ���
(3)����EF,�ӳ�AE��BF�ཻ�ڵ�C,Ȼ����(2)ͬ����֤.
�⣺(1)EF��BE+DF��֤�����£�
����ABE����ADG��
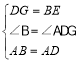 ��
��
���ABE�ա�ADG(SAS)��
��AE��AG����BAE����DAG��
�ߡ�EAF��![]() ��BAD��
��BAD��
���GAF����DAG+��DAF����BAE+��DAF����BAD����EAF����EAF��
���EAF����GAF��
����AEF����GAF��
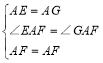 ��
��
���AEF�ա�AGF(SAS)��
��EF��FG��
��FG��DG+DF��BE+DF��
��EF��BE+DF��
�ʴ�Ϊ EF��BE+DF��
(2)����EF��BE+DF��Ȼ������
���ɣ��ӳ�FD����G��ʹDG��BE������AG����ͼ2��
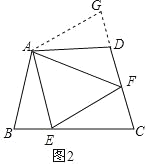
����ABE����ADG��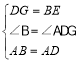 ��
��
���ABE�ա�ADG(SAS)��
��AE��AG����BAE����DAG��
�ߡ�EAF��![]() ��BAD��
��BAD��
���GAF����DAG+��DAF����BAE+��DAF����BAD����EAF����EAF��
���EAF����GAF��
����AEF����GAF��
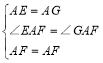 ��
��
���AEF�ա�AGF(SAS)��
��EF��FG��
��FG��DG+DF��BE+DF��
��EF��BE+DF��
(3)��ͼ3������EF���ӳ�AE��BF�ཻ�ڵ�C��
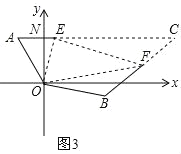
�ߡ�AOB��30��+90��+(90����70��)��140������EOF��70����
���EOF��![]() ��AOB��
��AOB��
�֡�OA��OB����OAC+��OBC��(90����30��)+(70��+50��)��180����
�����̽�������е�������
�����EF��AE+BF������
��EF��2��(45+60)��210(����)��
�𣺴�ʱ����֮ͧ��ľ�����210���