题目内容
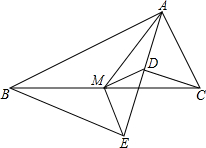
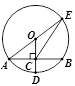
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
(A)2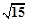 (B)8 (C)2
(B)8 (C)2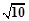 (D)2
(D)2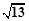
(A)2
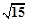 (B)8 (C)2
(B)8 (C)2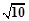 (D)2
(D)2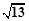

D.
试题分析:连结BE,设⊙O的半径为R,如图,
∵OD⊥AB,
∴AC=BC=
 AB=
AB= ×8=4,
×8=4,在Rt△AOC中,OA=R,OC=R-CD=R-2,
∵OC2+AC2=OA2,
∴(R-2)2+42=R2,解得R=5,
∴OC=5-2=3,
∴BE=2OC=6,
∵AE为直径,
∴∠ABE=90°,
在Rt△BCE中,CE=

故选D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
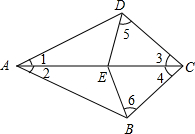
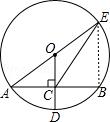
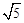 , “日”字形的对角线长都为
, “日”字形的对角线长都为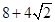 ,则八角形纸板的边长为 .
,则八角形纸板的边长为 .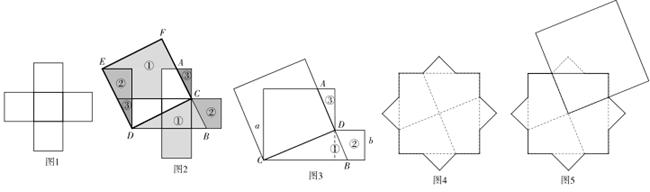
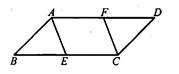
 ,求△CAF的面积.
,求△CAF的面积.