题目内容
【题目】画图题：
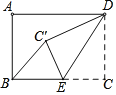
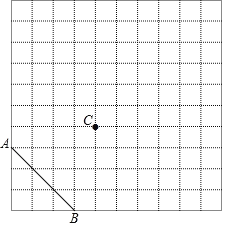
（1）在如图所示的方格纸中，经过线段AB外一点C，不用量角器与三角尺，仅用直尺，画线段AB的垂线CE和平行线CH．
（2）判断CE、CH的位置关系是 ．
（3）连接AC和BC，若小正方形的边长为a，求三角形ABC的面积．（用含a的代数式表示）．
【答案】（1）答案见解析；（2）CE⊥CH；（3）
a2．
【解析】
（1）根据正方形的性质，在网格图中找和点C是对角线的点E，连接CE就是AB的垂线，根据对称性找到点H，连接CH即是所求；
（2）根据（1）中作图的方法，结合平行的性质，可以得出CE⊥CH；
（3）根据割补法，三角形ABC的面积看成正方形的面积减去三个直角三角形的面积即可．
解：（1）如图，根据正方形的性质，找到点E连接CE即为所求作的AB的垂线，利用对称性找到点H，连接CH即为所求AB的平行线；
（2）∵CE⊥AB，CH∥AB，
∴∠ECH=90°，
∴CH⊥CE
CE、CH的位置关系是CE⊥CH．
故答案为：CE⊥CH；
（3）如图，连接AC和BC，
∵小方格的边长为a，则三角形ABC的面积为
=16a2﹣
×（3a）2﹣2××a×4a=a2．
故答案为：a2．
轻松暑假总复习系列答案
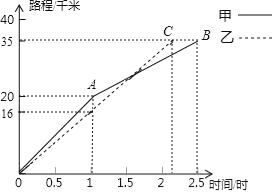
【题目】为了发展学生的核心素养，培养学生的综合能力，某中学利用“阳光大课间”，组织学生积极参加丰富多彩的课外活动，学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等，其中射击队在某次训练中，甲、乙两名队员各射击10发子弹，成绩用下面的折线统计图表示：（甲为实线，乙为虚线）
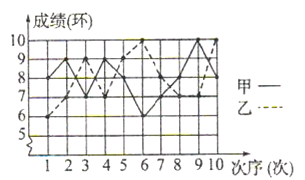
（1）依据折线统计图，得到下面的表格：
射击次序（次） | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲的成绩（环） | 8 | 9 | 7 | 9 | 8 | 6 | 7 |
| 10 | 8 |
乙的成绩（环） | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 |
| 10 |
其中
________，
________；
（2）甲成绩的众数是________环，乙成绩的中位数是________环；
（3）请运用方差的知识，判断甲、乙两人谁的成绩更为稳定？
（4）该校射击队要参加市组织的射击比赛，已预选出2名男同学和2名女同学，现要从这4名同学中任意选取2名同学参加比赛，请用列表或画树状图法，求出恰好选到1男1女的概率.
