题目内容
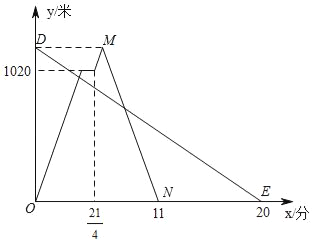
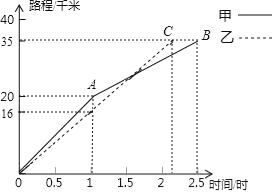
【题目】2018年,广州国际龙舟邀请赛于6月23日在中山大学北门广场至广州大桥之间的珠江河段举行.上午8时,参赛龙舟同时出发,甲、乙两队在比赛中,路程y(千米)与时间x(小时)的函数关系如图所示,甲队在上午11时30分到达终点.
(1)在比赛过程中,乙队何时追上甲队?
(2)在比赛过程中,甲、乙两队何时相距最远?
【答案】(1)出发1小时40分(或者说上午10点40分)时,乙队追上甲队(2)在比赛过程中,甲、乙两队在出发后1小时(或者上午9时)相距最远.
【解析】
(1)从图象看,甲队是OA和AB段,乙队是OC段,分别通过相关点的坐标,求出它们的解析式,联立OC与AB解析式即可解出交点,交点横坐标即为乙队追上甲队的时间;
(2)从图象看,一小时的时候两者相距较远,再将其与乙队到达终点时的距离比较即可.
解:(1)对于乙队,x=1时,y=16x,
∴OC解析式为:y=16x.
对于甲队,
当0≤x≤1时,令y=k1x,将(1,20)代入得:k1=20,
∴y=20x;
当x>1时,设AB解析式为:y=k2x+b,
将(1,20)和(2.5,35)分别代入得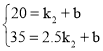 ,解得
,解得![]() ,
,
∴y=10x+10.
联立OC与AB解析式得![]() ,解得x=
,解得x=![]()
∴出发1小时40分(或者说上午10点40分)时,乙队追上甲队.
(2)1小时内,两队相距最远为20﹣16=4米,之后到相遇,距离在变小;
乙队追上甲队后,两队的距离为:16x﹣(10x+10)=6x﹣10,
当x值取最大,
即当16x=35,x=![]() 时,6x﹣10=6×
时,6x﹣10=6×![]() ﹣10=3.125<4.
﹣10=3.125<4.
∴在比赛过程中,甲、乙两队在出发后1小时(或者上午9时)相距最远.

练习册系列答案
相关题目