��Ŀ����
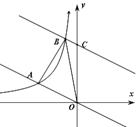
����Ŀ����ͼ1,��ƽ��ֱ������ϵ��,ֱ��![]() ��������
��������![]() ����
����![]() ���㣬����
���㣬����![]() ,
,![]() .����������
.����������![]() �ύ�ڵ�
�ύ�ڵ�![]() ,��
,��![]() �ύ����һ��
�ύ����һ��![]() .
.

(1)��![]() ��ֵ���������ߵĽ���ʽ;
��ֵ���������ߵĽ���ʽ;
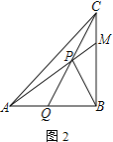
(2)��ͼ2.����![]() Ϊ�߶�
Ϊ�߶�![]() �ϵ�һ����(����
�ϵ�һ����(����![]() �غ�).�ֱ���
�غ�).�ֱ���![]() ��
��![]() Ϊб��,��ֱ��
Ϊб��,��ֱ��![]() ��ͬ��������ֱ����
��ͬ��������ֱ����![]() �͵���ֱ����
�͵���ֱ����![]() ,����
,����![]() ,��ȷ����
,��ȷ����![]() ������ʱ
������ʱ![]() �������.
�������.
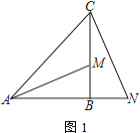
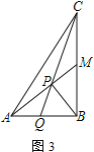
(3)��ͼ3.����![]() ��
��![]() ,���߶�
,���߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ,ʹ����
,ʹ����![]() Ϊ���������������
Ϊ���������������![]() ����,������,��ֱ��д����
����,������,��ֱ��д����![]() ������;��������,��˵������.
������;��������,��˵������.
���𰸡���1��![]() ����2����
����2����![]() ����
����![]() ʱ��
ʱ��![]() ���ʱ
���ʱ![]() ,����
,����![]() ����3�����ڵ�
����3�����ڵ�![]() ����Ϊ
����Ϊ![]() ��
��![]() .
.
����������1����A��B�������һ�κ�������ʽ���m��n��ֵ��ȷ����A��B������������κ�������ʽ���b��c��ֵ������
��2���ɵ���ֱ�ǡ�APM�͵���ֱ�ǡ�DPN���õ���MPNΪֱ��������ֱ�DZ߳˻���һ���ʾ��������MPN��������ö��κ�������ȷ����������������ʱP�����꼴����
��3��������������������������Ƶñ��������AQ�ij������������ľ��빫ʽ���Q���꼴�ɣ�
��1����A��m��0����B��4��n������y=x��1����m=1��n=3����A��1��0����B��4��3����
��y=��x2+bx+c������A���B����![]() �������
�������![]() ������κ�������ʽΪy=��x2+6x��5��
������κ�������ʽΪy=��x2+6x��5��
��2����ͼ2����APM���DPN��Ϊ����ֱ�������������APM=��DPN=45�㣬���MPN=90�㣬���MPNΪֱ�����������x2+6x��5=0���õ�x=1��x=5����D��5��0������DP=5��1=4����AP=m������DP=4��m����PM=![]() m��PN=
m��PN=![]() ��4��m������S��MPN=
��4��m������S��MPN=![]() PMPN=
PMPN=![]() ��
��![]() m��
m��![]() ��4��m��=��
��4��m��=��![]() m2��m=��
m2��m=��![]() ��m��2��2+1���൱m=2����AP=2ʱ��S��MPN�������ʱOP=3����P��3��0����
��m��2��2+1���൱m=2����AP=2ʱ��S��MPN�������ʱOP=3����P��3��0����
��3����������ֱ��CD����ʽΪy=x��5����Q��x��x��5���������������BAD=��ADC=45�㣬���������������
������ABD�ס�DAQʱ��![]() =
=![]() ����
����![]() =
=![]() �������AQ=
�������AQ=![]() ���������ľ��빫ʽ������x��1��2+��x��5��2=
���������ľ��빫ʽ������x��1��2+��x��5��2=![]() �������x=
�������x=![]() ����ʱQ��
����ʱQ��![]() ����
����![]() ����
����
�ڵ���ABD�ס�DQAʱ��![]() =1����AQ=
=1����AQ=![]() ������x��1��2+��x��5��2=10�������x=2����ʱQ��2����3����
������x��1��2+��x��5��2=10�������x=2����ʱQ��2����3����
��������Q��������2����3����![]() ����
����![]() ����
����