题目内容
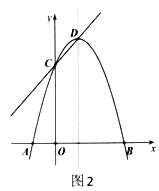
【题目】如图,二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 两点,并经过
两点,并经过![]() 点,已知
点,已知![]() 点坐标是
点坐标是![]() ,
,![]() 点坐标是
点坐标是![]() .
.
(1)求二次函数的解析式;
(2)求函数图象的顶点坐标及![]() 点的坐标;
点的坐标;
(3)二次函数的对称轴上是否存在一点![]() ,使得
,使得![]() 的周长最小?若
的周长最小?若![]() 点存在,求出
点存在,求出![]() 点的坐标,若
点的坐标,若![]() 点不存在,请说明理由.
点不存在,请说明理由.
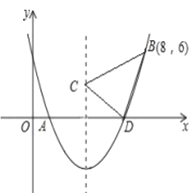
【答案】(1)![]()
(2)(4,2),(6,0)
(3)存在,C(4,2)
【解析】
(1)只需运用待定系数法就可求出二次函数的解析式;
(2)只需运用配方法就可求出抛物线的顶点坐标,只需令y=0就可求出点D的坐标;
(3)连接CA,由于BD是定值,使得△CBD的周长最小,只需CD+CB最小,根据抛物线是轴对称图形可得CA=CD,只需CA+CB最小,根据“两点之间,线段最短”可得:当点A、C、B三点共线时,CA+CB最小,只需用待定系数法求出直线AB的解析式,就可得到点C的坐标.
(1)把A(2,0),B(8,6)代入![]() ,得
,得
![]()

解得![]()
∴二次函数的解析式为![]()
故答案为:![]()
(2)由![]() 得二次函数图象的顶点坐标为(4,2)
得二次函数图象的顶点坐标为(4,2)
令y=0,得![]()
解得:x1=2,x2=6,
∴D点的坐标为(6,0).
故答案为:(4,2),(6,0)
(3)二次函数的对称轴上存在一点C,使得△CBD的周长最小.
连接CA,如图,
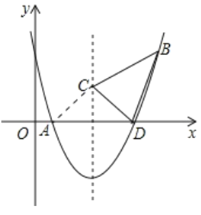
∵点C在二次函数的对称轴x=4上,
∴xC=4,CA=CD,
∴△CBD的周长=CD+CB+BD=CA+CB+BD,
根据“两点之间,线段最短”,可得当点A、C、B三点共线时,CA+CB最小,此时,由于BD是定值,因此△CBD的周长最小.
设直线AB的解析式为y=mx+n,
把A(2,0)、B(8,6)代入y=mx+n,得
![]()
解得![]()
∴直线AB的解析式为y=x2
当x=4时,y=42=2,
∴当二次函数的对称轴上点C的坐标为(4,2)时,△CBD的周长最小.
故答案为:存在,C(4,2)

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目