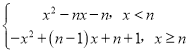题目内容
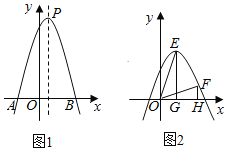
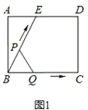
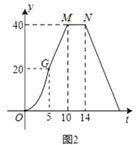
【题目】如图1所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止,设P、Q同时出发t秒时,BPQ的面积为ycm2,已知y与t的函数关系图象如图2所示(其中曲线OG为抛物线的一部分,其余各部分均为线段)所示,则下列结论:①BEBC;②当t6秒时,ABE PQB;③点P运动了18秒;④当t![]() 秒时,ABE∽QBP.其中正确的是( ).
秒时,ABE∽QBP.其中正确的是( ).
A.①②B.①③④C.③④D.①②④
【答案】A
【解析】
选项①正确.根据图中的信息,求出BE、AD的值即可判断;
选项②正确.根据SAS即可判断;
选项③错误.求出BE+DE+CD的值,可知点P运动了22秒;
选项④错误.当t=![]() 秒时,点P在线段DE上,点Q与点C重合,此时∠PQB≠90°,由此即可判断.
秒时,点P在线段DE上,点Q与点C重合,此时∠PQB≠90°,由此即可判断.
解:由图像可知,AD=BC=5×2=10,BE=1×10=10,ED=4×1=4,AE=10-4=6,
∴BE=BC,故①正确,
如下图所示,当t=6秒时,点P在BE上,点Q静止于点C处,
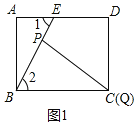
在△ABE与△PQB中,

∴△ABE≌△PQB(SAS),故②正确,
在Rt△ABE中,![]()
∴BE+DE+DC=10+4+8=22,
∴点P运动了22秒,故③错误,
当t=![]() 秒时,点P在线段DE上,点Q与点C重合,此时∠PQB≠90°,
秒时,点P在线段DE上,点Q与点C重合,此时∠PQB≠90°,
∴△ABE与△QBP不相似,故④错误.
∴①②正确.
故选:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目