Question

【题目】如图，两根高度分别是米和米的直杆、竖直在水平地面上，相距米，现要从点拉一根绳索，接地后再拉到点处，为了节省绳索材料，请问：

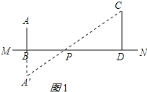
（1）根据你学过的知识，在地面上确定绳索接地的位置（用点表示），使绳索的长度最短.

（2）求绳索的最短长度（不计接头部分）．

Answer 1

【答案】（1）见解析；（2）绳索的最短长度为13米

【解析】

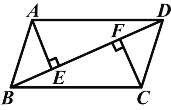
（1）作点A关于MN的对称点A′，连接A′C，交MN于P即可；

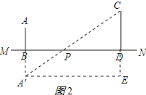
（2）作A′E∥MN，交CD的延长线于点E，由题意得出A′E＝BD＝12，DE＝A′B＝AB＝2，∠A′EC＝90°，得出CE＝CD＋CE＝5，由勾股定理得出A′C＝13（米），由轴对称的性质得出PA＝PA′，得出PA＋PC＝PA′＋PC＝A′C＝13米即可．

解：（1）作点关于的对称点，连接，交于，

点即为所求，如图所示：

（2）作，交的延长线于点，

如图所示：

由题意得：，，，

∵，

∴，

在中，由勾股定理得：（米），

由轴对称的性质得：，

∴米．

答：绳索的最短长度为米．