Question

【题目】如图1，在平面直角坐标系xoy中，点M在x轴的正半轴上，⊙M交x轴于A、B两点，交y轴于C、D两点，且C为弧AE的中点，AE交y轴于G点，若点A的坐标为（-1，0），AE=4

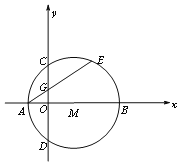
（1）求点C的坐标；

（2）连接MG、BC，求证：MG∥BC

Answer 1

【答案】(1)（0，4）．(2)证明见解析.

【解析】

试题分析：（1）求C点的坐标，即求出OC的长．根据垂径定理可得出弧CD=2弧AC，而题中已经告诉了C是弧AE的中点，即弧AE=2弧AC，即弧CD=弧AE，因此CD=AE，那么OC=AE=4，即可求出C点坐标；

（2）由于无法直接证明∠OMG=∠OBC来得出两直线平行，因此可通过相似三角形来求解，可设出圆的半径，然后分别求出OG、OM、OB的长，然后通过证OG、OM，OC、OB对应成比例来得出△OMG与△OBC相似来得出∠OMG=∠OBC，进行得出所求的结论.

试题解析：（1）∵直径AB⊥CD，

∴CO=CD，，

∵C为的中点，

∴，

∴，

∴CD=AE，

∴CO=CD=4，

∴C点的坐标为（0，4）．

（2）设半径AM=CM=r，则OM=r-2，

由OC2+OM2=MC2得：

42+（r-2）2=r2，

解得：r=5，

∴OM=r-OA=3

∵∠AOC=∠ANM=90°，

∠EAM=∠MAE，

∴△AOG∽△ANM，

∴，

∵MN=OM=3，

即，

∴OG=

∵，，

∴，

∵∠BOC=∠BOC，

∴△GOM∽△COB，

∴∠GMO=∠CBO，

∴MG∥BC．