Question

【题目】在△ABC中，∠BAC＝90°，AC＝AB，点D为直线BC上的一动点，以AD为边作△ADE（顶点A、D、E按逆时针方向排列），且∠DAE＝90°，AD＝AE，连接CE.

⑴ 如图1，若点D在BC边上（点D与B、C不重合），求∠BCE的度数.

⑵ 如图2，若点D在CB的延长线上，若DB＝5，BC＝7，求△ADE的面积．

Answer 1

【答案】（1）∠BCE＝90°；（2）.

【解析】试题分析：

（1）由已知条件证△ABD≌△ACE，可得∠ACE=∠B=45°，从而可得∠BCE=∠ACE+∠ACB=90°；

（2）同（1）由已知条件证△ABD≌△ACE，可得CE=BD=5及∠ACE=∠ABD=180°-45°=135°，从而可得∠DCE=∠ACE-∠ACB=90°，这样在Rt△DCE中由勾股定理可求得DE的长，再过点A作AF⊥DE于点F，由等腰三角形和直角三角形的性质可得AF=DE，这样就可由S△ADE=DEAF求得面积了.

试题解析：

(1)如图1，∵ ∠BAC＝90°，∠DAE＝90°,

∴ ∠BAD＋∠DAC＝90°，∠EAC＋∠DAC＝90°,

∴ ∠BAD＝∠EAC .

在△ABD和△ACE中， ，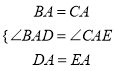

∴ △ABD≌△ACE （SAS）

∴ ∠ACE＝∠B

∵ ∠BAC＝90°

∴ ∠B＋∠ACB＝90°

∴ ∠ACE＋∠ACB＝90° 即：∠BCE＝90°.

(2) 如图2，过点A作AF⊥DE于点F.

∵ AD=AE，

∴ 点F是DE的中点.

∵ ∠DAE＝90°，

∴.

同（1）可证：△ABD≌△ACE，

∴EC=BD=5，∠ABD＝∠ACE=180°-∠ABC=135°，

∴∠DCE=∠ACE-∠ACB=90°，

又∵DC=BD+BC=5+7=12，

∴DE=.

∴AF=.

∴ △ADE的面积为＝