题目内容
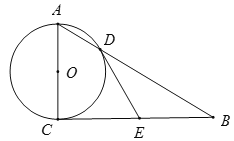
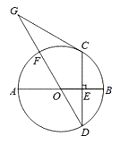
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°.
(1)求证:CG是⊙O的切线 (2)若CD=6,求GF的长
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)连接OC,根据三角形内角和定理可得∠DCG=180°-∠D-∠G=120°,再计算出∠GCO的度数可得OC⊥CG,进而得到CG是⊙O的切线;
(2)设EO=x,则CO=2x,再利用勾股定理计算出EO的长,进而得到CO的长,然后再计算出FG的长即可.
试题解析:(1)证明:连接OC.
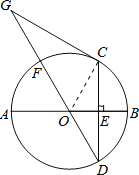
∵OC=OD,∠D=30°,
∴∠OCD=∠D=30°.
∵∠G=30°,
∴∠DCG=180°-∠D-∠G=120°.
∴∠GCO=∠DCG-∠OCD=90°.
∴OC⊥CG.
又∵OC是⊙O的半径.
∴CG是⊙O的切线.
(2)解:∵AB是⊙O的直径,CD⊥AB,
∴CE=![]() CD=3.
CD=3.
∵在Rt△OCE中,∠CEO=90°,∠OCE=30°,
∴EO=![]() CO,CO2=EO2+CE2.
CO,CO2=EO2+CE2.
设EO=x,则CO=2x.
∴(2x)2=x2+32.
解得x=±![]() (舍负值).
(舍负值).
∴CO=2![]() .
.
∴FO=2![]() .
.
在△OCG中,∵∠OCG=90°,∠G=30°,
∴GO=2CO=4![]() .
.
∴GF=GO-FO=2![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目