题目内容
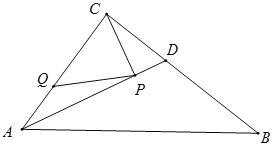
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的平分线.若
的平分线.若![]() ,
,![]() 分别是
分别是![]() 和
和![]() 上的动点,则
上的动点,则![]() 的最小值是__________.
的最小值是__________.
【答案】![]()
【解析】
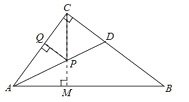
过点C作CM⊥AB交AB于点M,交AD于点P,过点P作PQ⊥AC于点Q,由AD是∠BAC的平分线.得出PQ=PM,这时PC+PQ有最小值,即CM的长度,运用勾股定理求出AB,再运用S△ABC=![]() ABCM=
ABCM=![]() ACBC,得出CM的值,即PC+PQ的最小值.
ACBC,得出CM的值,即PC+PQ的最小值.
如图,过点C作CM⊥AB交AB于点M,交AD于点P,过点P作PQ⊥AC于点Q,
∵AD是∠BAC的平分线.
∴PQ=PM,这时PC+PQ有最小值,即CM的长度,
∵AC=6,AB=10,∠ACB=90°,BC=8,S△ABC=![]() ABCM=
ABCM=![]() ACBC,
ACBC,
∴CM=![]() =
=![]() ,
,
即PC+PQ的最小值为![]() .
.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
【题目】学校举行图书节义卖活动,将所售款项捐给其他贫困学生.在这次义卖活动中,某班级售书情况如表:
售价 | 3元 | 4元 | 5元 | 6元 |
数目 | 14本 | 11本 | 10本 | 15本 |
下列说法正确的是( )
A. 该班级所售图书的总收入是226元
B. 在该班级所售图书价格组成的一组数据中,中位数是4
C. 在该班级所售图书价格组成的一纽数据中,众数是15
D. 在该班级所售图书价格组成的一组数据中,方差是2