题目内容
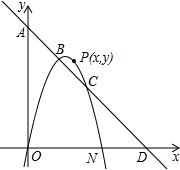
如图,抛物线y=ax2-5x+4a与x轴相交于点A、B,且经过点C(5,4).该抛物线顶点为P.
(1)求a的值和该抛物线顶点P的坐标.
(2)求△PAB的面积;
(3)若将该抛物线先向左平移4个单位,再向上平移2个单位,求出平移后抛物线的解析式.
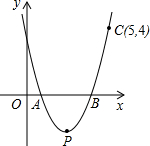
(1)求a的值和该抛物线顶点P的坐标.
(2)求△PAB的面积;
(3)若将该抛物线先向左平移4个单位,再向上平移2个单位,求出平移后抛物线的解析式.

(1)将C(5,4)的坐标代入抛物线解析式y=ax2-5x+4a,得a=1,
∴抛物线解析式y=x2-5x+4=(x-
)2-
∴抛物线顶点坐标为(
,-
);
(2)∵当y=x2-5x+4中y=0时,x1=1,x2=4,
∴A、B两点的坐标为A(1,0),B(4,0),△PAB的面积=
×3×
=
,
(3)∵抛物线原顶点坐标为(
,-
),平移后的顶点为(-
,-
),
∴平移后抛物线解析式y=(x+
)2-
;
∴抛物线解析式y=x2-5x+4=(x-
| 5 |
| 2 |
| 9 |
| 4 |
∴抛物线顶点坐标为(
| 5 |
| 2 |
| 9 |
| 4 |
(2)∵当y=x2-5x+4中y=0时,x1=1,x2=4,
∴A、B两点的坐标为A(1,0),B(4,0),△PAB的面积=
| 1 |
| 2 |
| 9 |
| 4 |
| 27 |
| 8 |
(3)∵抛物线原顶点坐标为(
| 5 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
∴平移后抛物线解析式y=(x+
| 3 |
| 2 |
| 1 |
| 4 |

练习册系列答案
 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目


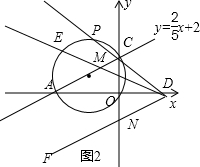
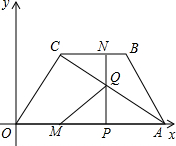
 的速度向点B运动.若点M、N同时开始运动,其中一点到达终点,另一点也停止运动,运动时间为t(t>0).过点N作NP⊥BC与P,交BD于点Q.
的速度向点B运动.若点M、N同时开始运动,其中一点到达终点,另一点也停止运动,运动时间为t(t>0).过点N作NP⊥BC与P,交BD于点Q.