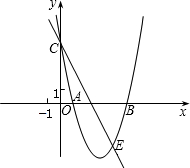
题目内容
已知:直线y=2x+6与x轴和y轴分别交于A、C两点,抛物线y=-x2+bx+c经过点A、C,点B是抛物 线与x轴的另一个交点.
线与x轴的另一个交点.
(1)求抛物线的解析式及B的坐标;
(2)设点P是直线AC上一点,且S△ABP:S△BPC=1:3,求点P的坐标;
(3)直线y=
x+a与(1)中所求的抛物线交于M、N两点,问:是否存在a的值,使得∠MON=90°?若存在,求出a的值;若不存在,请说明理由.
 线与x轴的另一个交点.
线与x轴的另一个交点.(1)求抛物线的解析式及B的坐标;
(2)设点P是直线AC上一点,且S△ABP:S△BPC=1:3,求点P的坐标;
(3)直线y=
| 1 |
| 2 |
(1)当x=0时,y=6,
∴C(0,6),
当y=0时,x=-3,
∴A(-3,0),
∵抛物线y=-x2+bx+c经过点A、C,
∴
,
解得:
.
∴抛物线的解析式为y=-x2-x+6,
当y=0时,整理得x2+x-6=0,
解得:x1=2,x2=-3,
∴点B(2,0).
(2)过点B作BD⊥AC,D为垂足,
∵S△ABP:S△BPC=1:3,
∴
=
,
∴AP:PC=1:3
由勾股定理,得AC=
=3

当点P为线段AC上一点时,过点P作PH⊥x轴,点H为垂足,
∴
=
=
∴PH=
,
∴
=2x+6,
∴x=-
,
∴点P(-
,
)
当点P在CA延长线时,作PG⊥x轴,点G为垂足
∵AP:PC=1:3
∴AP:AC=1:2,
∴
=
=
,
∴PG=3,
∴-3=2x+6
x=-
,
∴点P(-
,-3).
(3)存在a的值,使得∠MON=90°,
设直线y=
x+a与抛物线y=-x2-x+6的交点为M(xM,yM),N(xN,yN)(M在N左侧)
则
为方程组
的解
分别过点M、N作MM’⊥x轴,NN′⊥x轴,点M、N为垂足.
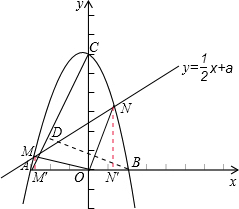 ∴M′(xM,0),N′(xN,0),
∴M′(xM,0),N′(xN,0),
∴OM′=-xMON′=xN
∵∠MON=90°,
∴∠MOM′+∠NON′=90°,
∵∠M′MO+∠MOM′=90°,
∴∠M’MO=∠NON’
∴Rt△MM′O∽Rt△ON′N,
∴
=
,
∴MM′•NN′=ON′•OM′,
∴-xM•xN=yM•yN,
由方程组消去y整理,得:x2+
x+a-6=0.
∴xM、xN是方程x2+
x+a-6=0的两个根,
由根与系数关系得,xM+xN=-
,xM•xN=a-6
又∵yM•yN=(
xM+a)(
xN+a)=
xM•xN+
(xM+xN)+a2=
(a-6)-
a+a2
∴-(a-6)=
(a-6)-
a+a2,
整理,得2a2+a-15=0
解得a1=-3,a2=
∴存在a值,使得∠MON=90°,其值为a=-3或a=
.
∴C(0,6),
当y=0时,x=-3,
∴A(-3,0),
∵抛物线y=-x2+bx+c经过点A、C,
∴
|
解得:
|
∴抛物线的解析式为y=-x2-x+6,
当y=0时,整理得x2+x-6=0,

解得:x1=2,x2=-3,
∴点B(2,0).
(2)过点B作BD⊥AC,D为垂足,
∵S△ABP:S△BPC=1:3,
∴
| ||
|
| 1 |
| 3 |
∴AP:PC=1:3
由勾股定理,得AC=
| AO2+CO2 |
| 5 |

当点P为线段AC上一点时,过点P作PH⊥x轴,点H为垂足,
∴
| PH |
| OC |
| AP |
| AC |
| 1 |
| 4 |
∴PH=
| 3 |
| 2 |
∴
| 3 |
| 2 |
∴x=-
| 9 |
| 4 |
∴点P(-
| 9 |
| 4 |
| 3 |
| 2 |
当点P在CA延长线时,作PG⊥x轴,点G为垂足
∵AP:PC=1:3

∴AP:AC=1:2,
∴
| PG |
| OC |
| AP |
| AC |
| 1 |
| 2 |
∴PG=3,
∴-3=2x+6
x=-
| 9 |
| 2 |
∴点P(-
| 9 |
| 2 |
(3)存在a的值,使得∠MON=90°,
设直线y=
| 1 |
| 2 |
则
|
|
为方程组
|
分别过点M、N作MM’⊥x轴,NN′⊥x轴,点M、N为垂足.
 ∴M′(xM,0),N′(xN,0),
∴M′(xM,0),N′(xN,0),∴OM′=-xMON′=xN
∵∠MON=90°,
∴∠MOM′+∠NON′=90°,
∵∠M′MO+∠MOM′=90°,
∴∠M’MO=∠NON’
∴Rt△MM′O∽Rt△ON′N,
∴
| MM′ |
| ON′ |
| OM′ |
| NN′ |
∴MM′•NN′=ON′•OM′,
∴-xM•xN=yM•yN,
由方程组消去y整理,得:x2+
| 3 |
| 2 |
∴xM、xN是方程x2+
| 3 |
| 2 |
由根与系数关系得,xM+xN=-
| 3 |
| 2 |
又∵yM•yN=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| a |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
∴-(a-6)=
| 1 |
| 4 |
| 3 |
| 4 |
整理,得2a2+a-15=0
解得a1=-3,a2=
| 5 |
| 2 |
∴存在a值,使得∠MON=90°,其值为a=-3或a=
| 5 |
| 2 |

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目




 的速度向点B运动.若点M、N同时开始运动,其中一点到达终点,另一点也停止运动,运动时间为t(t>0).过点N作NP⊥BC与P,交BD于点Q.
的速度向点B运动.若点M、N同时开始运动,其中一点到达终点,另一点也停止运动,运动时间为t(t>0).过点N作NP⊥BC与P,交BD于点Q.