题目内容
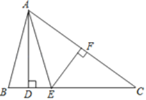
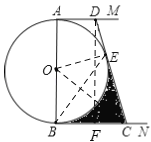
【题目】如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,E为⊙O上一点,过点E作直线DC分别交AM,BN于点D,C,且CB=CE.
(1)求证:DA=DE;
(2)若AB=6,CD=4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

【答案】(1)证明见解析;(2)![]()
【解析】(1)连接OE,BE,根据已知条件证明CD为⊙O的切线,然后再根据切线长定理即可证明DA=DE;
(2) 如图,连接OC,过点D作DF⊥BC于点F,根据S阴影部分=S四边形BCEO﹣S扇形OBE,利用分割法即可求得阴影部分的面积.
(1)如图,连接OE、BE,
∵OB=OE,
∴∠OBE=∠OEB.
∵BC=EC,
∴∠CBE=∠CEB,
∴∠OBC=∠OEC.
∵BC为⊙O的切线,
∴∠OEC=∠OBC=90°;
∵OE为半径,
∴CD为⊙O的切线,
∵AD切⊙O于点A,
∴DA=DE;
(2)如图,连接OC,过点D作DF⊥BC于点F,则四边形ABFD是矩形,
∴AD=BF,DF=AB=6,
∴DC=BC+AD=4![]() ,
,
∵CF=![]() =2
=2![]() ,
,
∴BC﹣AD=2![]() ,
,
∴BC=3![]() ,
,
在直角△OBC中,tan∠BOC=![]() =
=![]() ,
,
∴∠BOC=60°.
在△OEC与△OBC中,
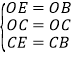 ,
,
∴△OEC≌△OBC(SSS),
∴∠BOE=2∠BOC=120°,
∴S阴影部分=S四边形BCEO﹣S扇形OBE=2×![]() BCOB﹣
BCOB﹣![]() =9
=9![]() ﹣3π.
﹣3π.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目