题目内容
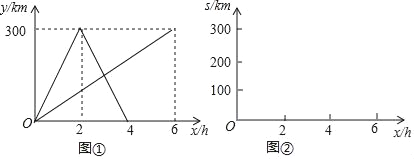
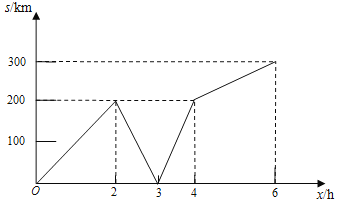
【题目】快车和慢车同时从甲地出发，匀速行驶，快车到达乙地后，原路返回甲地，慢车到达乙地停止．图①表示两车行驶过程中离甲地的路程y（km）与出发时间x（h）的函数图象，请结合图①中的信息，解答下列问题：
（1）快车的速度为 km/h，慢车的速度为 km/h，甲乙两地的距离为 km；
（2）求出发多长时间，两车相距100km；
（3）若两车之间的距离为s km，在图②的直角坐标系中画出s（km）与x（h）的函数图象．
【答案】（1）150，50，300；（2）1 h或2.5h或3.5h；（3）图象见解析.
【解析】分析：（1）观察函数图象可得出甲、乙两地间的距离，根据数量关系速度=路程÷时间即可得出快、慢两车的速度；
（2）根据图象找出点的坐标，利用待定系数法可求出线段解析式，由此即可得出结论；
（3）根据两车相遇结合t=0、2、3、4，6可找出关键点，依此画出函数图象即可．
详解：（1）快车的速度为300÷2=150km/h，慢车的速度为：300÷6=50km/h，甲乙两地的距离为300km，
故答案为：150，50，300；
（2）快车在行驶过程中离A地的路程y1与时间x的函数关系式：
当0≤x＜2时，y1=150x，
当2≤x≤4时，y1=300-150（x-2），即y1=600-150x．
慢车在行驶过程中离A地的路程y2与时间x的函数关系式：
当0≤x≤6时，y2=50x，
由题意，得
①当0≤x＜2时，y1-y2=100，150x-50x=100，解得x=1；
②当2≤x＜3时，y1-y2=100，600-150x-50x=100，解得x=2.5；
③当3≤x＜4时，y2-y1=100，50x-（600-150x）=100，解得x=3.5；
④当4≤x≤6时，两车相距大于100km．
答：出发1h或2.5h或3.5h后，两车相距100km；
（3）s与x的函数图象如图所示：
【题目】某商场试销一种成本为50元/件的
恤．经试销发现，销售量
（件）与销售单价
（元/件）符合一次函数关系，试销数据如下表：
售价（元/件） | …… | 55 | 60 | 70 | …… |
销量（件） | …… | 75 | 70 | 60 | …… |
（1）求一次函数
的表达式；
（2）若该商场获得利润为W元，试写出利润W与销售单价
之间的关系式；销售单价定为多少时，商场可获得最大利润，最大利润是多少？
【题目】某班同学响应“阳光体育运动”号召，利用课外活动积极参加体育锻炼，每位同学从长跑、铅球、立定跳远、篮球定点投篮中任选一项进行了训练，训练前后都进行了测试，现将项目选择情况及训练后篮球定点投篮进球数进行整理，作出如下统计图表．
训练后篮球定点投篮测试进球统计表：
进球数（个） | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
（1）选择长跑训练的人数占全班人数的百分比是 ，该班共有同学 人．
（2）求训练后篮球定点投篮人均进球数为多少个？
（3）根据测试资料，参加篮球定点投篮的学生训练后比训练前的人均进球增加了25%，求参加训练之前的人均进球数．
