题目内容
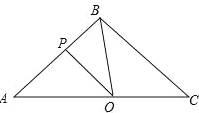
【题目】如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.
(1)当x为何值时,PQ∥BC;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)△APQ能否与△CQB相似?若能,求出时间x的值;若不能,说明理由.
【答案】(1)x=![]() ;(2)
;(2)![]() =2;(3)x的值是
=2;(3)x的值是![]() 或5.
或5.
【解析】试题分析:(1)当PQ∥BC时,根据平行线分线段成比例定理,可得出关于AP,PQ,AB,AC的比例关系式,我们可根据P,Q的速度,用时间x表示出AP,AQ,然后根据得出的关系式求出x的值;
(2)我们先看当S△BCQ:S△ABC=1:3时能得出什么条件,由于这两个三角形在AC边上的高相等,那么他们的底边的比就应该是面积比,由此可得出CQ:AC=1:3,那么CQ=10cm,此时时间x正好是(1)的结果,那么此时PQ∥BC,由此可根据平行这个特殊条件,得出三角形APQ和ABC的面积比,然后再根据三角形PBQ的面积=三角形ABC的面积-三角形APQ的面积-三角形BQC的面积来得出三角形BPQ和三角形ABC的面积比,由此即可得;
(3)本题要分两种情况进行讨论.已知了∠A和∠C对应相等,那么就要分成AP和CQ对应成比例以及AP和BC对应成比例两种情况来求x的值.
试题解析:
试题解析:(1)由题意得,PQ//BC,则AP:AB=AQ:AC,AP=4x, AQ=30﹣3x,
![]() ,解得x=
,解得x=![]() ;
;
(2)∵S△BCQ:S△ABC=1:3,
∴CQ:AC=1:3,CQ=10cm,
∴时间用了![]() 秒,AP=
秒,AP=![]() cm,
cm,
∵由(1)知,此时PQ平行于BC,
∴△APQ∽△ABC,相似比为![]() ,
,
∴S△APQ:S△ABC=4:9,∴S△APQ= ![]() S△ABC,
S△ABC,
∴四边形PQCB与三角形ABC面积比为5:9,即S四边形PQCB=![]() S△ABC,
S△ABC,
又∵S△BCQ:S△ABC=1:3,即S△BCQ=![]() S△ABC,
S△ABC,
∴S△BPQ=S四边形PQCB﹣S△BCQ═![]() S△ABC﹣
S△ABC﹣![]() S△ABC=
S△ABC=![]() S△ABC,
S△ABC,
∴![]() =
=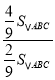 =2;
=2;
(3)假设两三角形可以相似,
情况1:当△APQ∽△CQB时,CQ:AP=BC:AQ,即有![]() ,
,
解得x=![]() ,
,
经检验,x=![]() 是原分式方程的解,
是原分式方程的解,
情况2:当△APQ∽△CBQ时,CQ:AQ=BC:AP,即有![]() ,
,
解得x=5,或x=-10(不合题意,舍去),
经检验,x=5是原分式方程的解,
综上所述,时间x的值是![]() 或5.
或5.

 名校课堂系列答案
名校课堂系列答案【题目】某商场计划购进甲、乙两种运动鞋,其中甲、乙两种运动鞋的进价和售价如表(进价大于50元)
运动鞋价格 | 甲 | 乙 |
进价(元/双) | m | m﹣4 |
售价(元/双) | 160 | 150 |
已知:用3000元购进甲种运动鞋的数量比用2400元购进乙种运动鞋的数量多5.
(1)求m的值;
(2)设该商场应购进甲种运动鞋t双,两种鞋共200双,商场销售完这批鞋可获利y元,请求出y关于t的函数解析式;
(3)商场计划在(2)的条件下,总进价不低于19520元,且不超过19532元,问该专卖店有哪几种进货方案?
(4)求该专卖店要获得最大利润的进货方案及最大利润.