题目内容
在锐角△ABC中，已知BC=6，∠C=60°，sinA=0.8，求AB和AC的长．（结果保留根号）
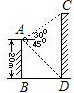
如图所示：作BD⊥AC于D．
∵∠C=60°，BC=6，
∴sin60°=
，
∴
=
，
∴BD=3
，
∴CD=BC•cos60°=6×
=3，
在Rt△ABD中，
=0.8，
=0.8，
AB=
，
AD=
=
=
，
∴AC=3+
=
．
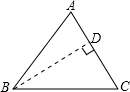
∵∠C=60°，BC=6，
∴sin60°=
| BD |
| BC |
∴
| ||
| 2 |
| BD |
| 6 |
∴BD=3
| 3 |
∴CD=BC•cos60°=6×
| 1 |
| 2 |
在Rt△ABD中，
| BD |
| AB |
3
| ||
| AB |
AB=
15
| ||
| 4 |
AD=
| AB2-BD2 |
(
|
9
| ||
| 4 |
∴AC=3+
9
| ||
| 4 |
12+9
| ||
| 4 |
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
