题目内容
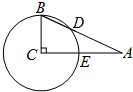 如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则
如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则 |
| BD |
| A、25° | B、30° |
| C、50° | D、65° |
考点:圆心角、弧、弦的关系
专题:
分析:连接CD,先根据直角三角形的性质求出∠ABC的度数,由等腰三角形的性质得出∠CDB的度数,根据三角形内角和定理求出∠BCD的度数,由圆心角、弧、弦的关系即可得出结论.
解答: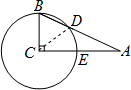 解:连接CD,
解:连接CD,
∵在△ABC中,∠C=90°,∠A=25°,
∴∠ABC=90°-25°=65°,
∵BC=CD,
∴∠CDB=∠ABC=65°,
∴∠BCD=180°-∠CDB-∠CBD=180°-65°-65°=50°,
∴
=50°.
故选C.
 解:连接CD,
解:连接CD,∵在△ABC中,∠C=90°,∠A=25°,
∴∠ABC=90°-25°=65°,
∵BC=CD,
∴∠CDB=∠ABC=65°,
∴∠BCD=180°-∠CDB-∠CBD=180°-65°-65°=50°,
∴
 |
| BD |
故选C.
点评:本题考查的是圆心角、弧、弦的关系,根据题意作出辅助线,构造出等腰三角形是解答此题的关键.

练习册系列答案
相关题目
 如图是教学用直角三角板,边AC=30cm,∠C=90°,∠BAC=30°,则BC长为( )
如图是教学用直角三角板,边AC=30cm,∠C=90°,∠BAC=30°,则BC长为( )A、30
| ||
B、20
| ||
C、10
| ||
D、5
|
如图(1)是长方形纸带,∠DEF=α,将纸带沿EF折叠成图(2),再沿BF折叠成图(3),则图(3)中的∠CFE的度数是( )
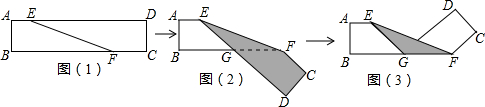

| A、2α |
| B、90°+2α |
| C、180°-2α |
| D、180°-3α |
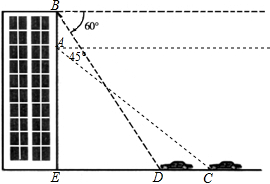 如图,小明在商贸大厦离地面25m高的A处看地面C处汽车,测得俯角为45°,小明上升5m后到B处看到该汽车行驶到D处,测得俯角为60°,若汽车在与该楼的垂直线上行驶,求汽车行驶的距离CD的长.(结果精确到0.1米,参考数据
如图,小明在商贸大厦离地面25m高的A处看地面C处汽车,测得俯角为45°,小明上升5m后到B处看到该汽车行驶到D处,测得俯角为60°,若汽车在与该楼的垂直线上行驶,求汽车行驶的距离CD的长.(结果精确到0.1米,参考数据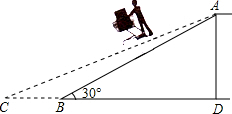 某商场为了方便顾客使用购物车,将滚动电梯由坡角30°的坡面改为坡度为1:2.4的坡面.如图,BD表示水平面,AD表示电梯的铅直高度,如果改动后电梯的坡面AC长为13米,求改动后电梯水平宽度增加部分BC的长(结果保留根号).
某商场为了方便顾客使用购物车,将滚动电梯由坡角30°的坡面改为坡度为1:2.4的坡面.如图,BD表示水平面,AD表示电梯的铅直高度,如果改动后电梯的坡面AC长为13米,求改动后电梯水平宽度增加部分BC的长(结果保留根号).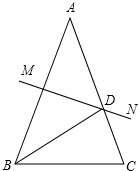 如图,在△ABC中,∠ABC=∠C,线段AB的垂直平分线MN交AC于点D.
如图,在△ABC中,∠ABC=∠C,线段AB的垂直平分线MN交AC于点D.