题目内容
【题目】(本题满分10分)已知四边形ABCD是矩形,对角线AC和BD相交于点P,若在矩形的上方加一个△DEA,且使DE∥AC,AE∥BD.
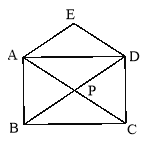
(1)求证:四边形DEAP是菱形;
(2)若AE=CD,求∠DPC的度数.
【答案】(1)见解析;(2)∠DPC=60°.
【解析】
试题(1)由题中由已知条件可得其为平行四边形,再加上一组邻边相等即为菱形.
(2)由(1)中的结论即可证明△PDC为等边三角形,从而得出∠DPC=60°.
试题解析:(1)∵DE∥AC,AE∥BD,
∴四边形DEAP为平行四边形,
∵ABCD为矩形,
∴AP=![]() AC,DP=
AC,DP=![]() BD,AC=BD,
BD,AC=BD,
∴AP=PD,PD=CP,
∴四边形DEAP为菱形;
∵四边形DEAP为菱形,
∴AE=PD,
∵AE=CD,
∴PD=CD,
∵PD=CP(上小题已证),
∴△PDC为等边三角形,
∴∠DPC=60°.

练习册系列答案
相关题目