题目内容
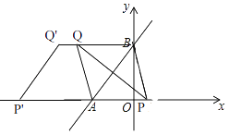
【题目】如图,直线![]() 与x轴交于点A,与y轴交于B,点P是x轴上的一个动点.
与x轴交于点A,与y轴交于B,点P是x轴上的一个动点.
(1)求A、B两点的坐标;
(2)当点P在x轴正半轴上,且△APB的面积为8时,求直线PB的解析式;
(3)点Q在第二象限,是否存在以A、B、P、Q为顶点的四边形是菱形?若存在,请求出点Q的坐标,若不存在,请说明理由.

【答案】(1)B(0,4),A(﹣3,0);(2)y=﹣x+4;(3)(﹣5,4)或(﹣![]() ,4)
,4)
【解析】
(1)根据坐标轴上点的特点即可得出结论;
(2)设出点P坐标,利用△PAB的面积建立方程求出P的坐标,最后用待定系数法求解即可;
(3)先判断出点Q在直线y=4上,再分两种情况讨论计算即可.
(1)令x=0时,y=4, ∴B(0,4),
令y=0时,![]() x+4=0,
x+4=0,
∴x=﹣3,
∴A(﹣3,0);
(2)设点P(m,0)(m>0), ∵A(﹣3,0),
∴AP=m﹣(﹣3)=m+3,
∵△APB的面积为8,
∴S△APB= ![]() AP×OB=
AP×OB=![]() (m+3)×4=8,
(m+3)×4=8,
∴m=1,
∴P(1,0),
∵B(0,4),
∴设直线PB的解析式为y=kx+4,
∴k+4=0,
∴k=﹣4,
∴直线PB的解析式为y=﹣x+4;
(3)如图,
∵以A、B、P、Q为顶点的四边形是菱形,且P在x轴上,
∴BQ∥AP,
∴点Q在直线y=4上,
由(1)知,A(﹣3,0),B(0,4),
∴AB=5,
∵点Q在第二象限内,
∴①当AB为菱形的边时,
∴BQ'=AB=5,
∴Q'(﹣5,4),
②当AB为菱形的对角线时,AB,PQ互相垂直平分,
∵直线AB的解析式为y= ![]() x+4,
x+4,
∴直线PQ的解析式为y=﹣ ![]() x+
x+ ![]() ,
,
当y=4时,则﹣ ![]() x+
x+ ![]() =4,
=4,
∴x=﹣![]() ,
,
∴Q(﹣ ![]() ,4),
,4),
∴满足条件的点Q的坐标为(﹣5,4)或(﹣ ![]() ,4).
,4).

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案【题目】为了解同学们每月零花钱数额,校园小记者随机调查了本校部分学生,并根据调查结果绘制出如下不完整的统计图表:
零花钱数额 | 人数(频数) | 频率 |
| 6 | 0.15 |
| 12 | 0.30 |
| 16 | 0.40 |
|
| 0.10 |
| 2 |
|

请根据以下图表,解答下列问题:
(1)这次被调查的人数共有__________人,![]() __________;
__________;
(2)计算并补全频数分布直方图;
(3)请估计该校1500名学生中每月零花钱数额低于90的人数.