题目内容
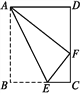
【题目】如图,在四边形ABCD中,∠A=104°-∠2,∠ABC=76°+∠2,BD⊥CD于D,EF⊥CD于F.
求证:∠1=∠2.请你完成下面证明过程.
证明:因为∠A=104°-∠2,∠ABC=76°+∠2,( )
所以 ∠A+∠ABC=104°-∠2+76°+∠2, ( 等式性质 )
即 ∠A+∠ABC=180°
所以 AD∥BC,( )
所以 ∠1=∠DBC,( )
因为 BD⊥DC,EF⊥DC,( )
所以 ∠BDC=90°,∠EFC=90°,( )
所以 ∠BDC=∠EFC,
所以 BD∥ ,( )
所以 ∠2=∠DBC,( )
所以 ∠1=∠2 ( ).
【答案】见解析.
【解析】首先观察已知条件中的角,不难发现:两个角互补,得平行.再根据平行线的性质得到有关角之间的关系,运用等量代换的方法证明最后的结论.
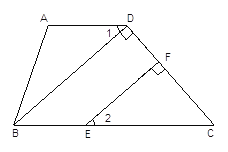
证明:因为∠A=104°-∠2,∠ABC=76°+∠2,(已知 )
所以∠A+∠ABC=104°-∠2+76°+∠2, ( 等式性质 )
即 ∠A+∠ABC=180°
所以 AD∥BC,(同旁内角互补,两直线平行)
所以 ∠1=∠DBC,(两直线平行,内错角相等)
因为 BD⊥DC,EF⊥DC,(已知)
所以 ∠BDC=90°,∠EFC=90°,( 垂直定义)
所以 ∠BDC=∠EFC,
所以 BD∥EF,(同位角相等,两直线平行)
所以 ∠2=∠DBC,(两直线平行,同位角相等)
所以 ∠1=∠2 (等量代换).


练习册系列答案
相关题目