ЬтФПФкШн
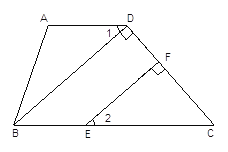
ЁОЬтФПЁПФГЙЋЫОЪдЯњвЛжжГЩБОЮЊ30дЊ/МўЕФаТВњЦЗЃЌАДЙцЖЈЪдЯњЪБЕФЯњЪлЕЅМлВЛЕЭгкГЩБОЕЅМлЃЌгжВЛИпгк80дЊ/МўЃЌЪдЯњжаУПЬьЕФЯњЪлСПyЃЈМўЃЉгыЯњЪлЕЅМлxЃЈдЊ/МўЃЉТњзуЯТБэжаЕФКЏЪ§ЙиЯЕЃЎ
ЃЈ1ЃЉЪдЧѓyгыxжЎМфЕФКЏЪ§БэДяЪНЃЛЃЈ2ЃЉЩшЙЋЫОЪдЯњИУВњЦЗУПЬьЛёЕУЕФУЋРћШѓЮЊSЃЈдЊЃЉЃЌЧѓSгыxжЎМфЕФКЏЪ§БэДяЪНЃЈУЋРћШѓ=ЯњЪлзмМл-ГЩБОзмМлЃЉЃЛ
ЃЈ2ЃЉЕБЯњЪлЕЅМлЖЈЮЊЖрЩйЪБЃЌИУЙЋЫОЪдЯњетжжВњЦЗУПЬьЛёЕУЕФУЋРћШѓзюДѓЃП
ЃЈ3ЃЉзюДѓУЋРћШѓЪЧЖрЩйЃПДЫЪБУПЬьЕФЯњЪлСПЪЧЖрЩйЃП
ЁОД№АИЁП
ЃЈ1ЃЉ
НтЃКЩшyгыxжЎМфЕФКЏЪ§ЙиЯЕТњзуy=kx+b
Абx=40ЃЌy=500ЃЛx=50ЃЌy=400
ЗжБ№ДњШыЩЯЪНЕУЃК
|
НтЕУ
|
Ёрy=-10x+900
ЁпБэжаЦфЫќЖдгІжЕЖМТњзуy=-10x+900
ЁрyгыxжЎМфЕФКЏЪ§ЙиЯЕЮЊвЛДЮКЏЪ§ЃЌЧвКЏЪ§БэДяЪНЮЊy=-10x+900ЃЈ30ЁмxЁм80ЃЉЃЛ
ЃЈ2ЃЉ
НтЃКУЋРћШѓS=ЃЈx-30ЃЉy=ЃЈx-30ЃЉЃЈ-10x+900ЃЉ=-10x2+1200x-27000ЃЈ30ЁмxЁм80ЃЉ
ЃЈ3ЃЉ
НтЃКдкS=-10x2+1200x-27000жа
Ёпa=-10ЃМ0ЃЌЁрЕБxЃН ![]() ЃН60ЪБ
ЃН60ЪБ
ЁрSзюДѓ=-10ЁС602+1200ЁС60-27000=9000ЃЈдЊЃЉ
ДЫЪБУПЬьЕФЯњЪлСПЮЊЃКy=-10ЁС60+900=300ЃЈМўЃЉЃЎ
ЁрЕБЯњЪлЕЅМлЖЈЮЊ60дЊ/МўЪБЃЌИУЙЋЫОЪдЯњетжжВњЦЗУПЬьЛёЕУЕФУЋРћШѓзюДѓЃЌзюДѓУЋРћШѓЪЧ9000дЊЃЌДЫЪБУПЬьЕФЯњЪлСПЪЧ300МўЃЎ
ЁОНтЮіЁПЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЫуГіКЏЪ§НтЮіЪНЃЛЃЈ2ЃЉзЂвтЖдЖўДЮКЏЪ§НтЮіЪНећРэЪБздБфСПЕФШЁжЕЗЖЮЇЃЛЃЈ3ЃЉЧѓКЏЪ§ЕФзюжЕЪБвЊНсКЯЪЕМЪЧщПі.

 аЁбЇбЇЯАКУАяЪжЯЕСаД№АИ
аЁбЇбЇЯАКУАяЪжЯЕСаД№АИ аЁбЇЭЌВНШ§СЗКЫаФУмОэЯЕСаД№АИ
аЁбЇЭЌВНШ§СЗКЫаФУмОэЯЕСаД№АИЁОЬтФПЁПФГЩЬГЁЭЖШы13 800дЊзЪН№ЙКНјМзЁЂввСНжжПѓШЊЫЎЙВ500ЯфЃЌПѓШЊЫЎЕФГЩБОМлКЭЯњЪлМлШчБэЫљЪОЃК
РрБ№/ЕЅМл | ГЩБОМл | ЯњЪлМл(дЊ/Яф) |
Мз | 24 | 36 |
вв | 33 | 48 |
(1)ИУЩЬГЁЙКНјМзЁЂввСНжжПѓШЊЫЎИїЖрЩйЯфЃП
(2)ШЋВПЪлЭъ500ЯфПѓШЊЫЎЃЌИУЩЬГЁЙВЛёЕУРћШѓЖрЩйдЊЃП