题目内容
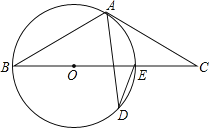
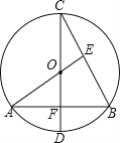
【题目】 如图，CD为⊙O直径，CD⊥AB于点F，AE⊥BC于E，AE过圆心O，且AO=1．则四边形BEOF的面积为（ ）
A.
B.
C.
D.
【答案】C
【解析】
根据垂径定理求出AF=BF，CE=BE，
，求出∠AOD=2∠C，求出∠AOD=2∠A，求出∠A=30°，解直角三角形求出OF和BF，求出OE、BE、BF，根据三角形的面积公式求出即可．
解：∵CD为直径，CD⊥AB，
∴，
∴∠AOD=2∠C，
∵CD⊥AB，AE⊥BC，
∴∠AFO=∠CEO=90°，
在△AFO和△CEO中
∴△AFO≌△CEO（AAS），
∴∠C=∠A，
∴∠AOD=2∠A，
∵∠AFO=90°，
∴∠A=30°，
∵AO=1，
∴OF=
AO=，AF=
OF=
，
同理CE=，OE=，
连接OB，
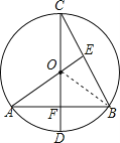
∵CD⊥AB，AE⊥BC，CD、AE过O，
∴由垂径定理得：BF=AF=，BE=CE=，
∴四边形BEOF的面积S=S△BFO+S△BEO=××+
=
，
故选：C．
练习册系列答案
相关题目
