题目内容
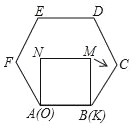
【题目】如图①，在正方形
中，
，
为对角线
上任意一点（不与
重合），连接
，过点作
，交线段
于点
.
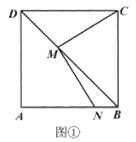
（1）求证：
；
（2）若
，求证：
；
（3）如图②，连接
交于点
．若
，求
的值．
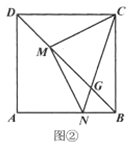
【答案】（1）见解析；（2）见解析；（3）
.
【解析】
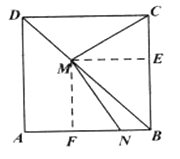
(1)如图，过
分别作
交
于点
，
交
于点
，则四边形
是平行四边形，先证明四边形
是正方形，继而证明
，即可得结论；
(2)由(1)得
，
，根据比例线段可得
，
，再根据可得
，从而求得AN、BN长即可得结论；
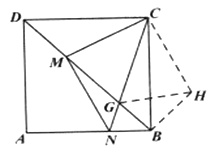
(3)把
绕点
逆时针旋转
得到
，连接
，
，进而可推导得出
，
，证明
是等腰直角三角形，继而证明
，可得MG=HG，根据题意设
，则
，根据勾股定理可求得
，再结合正方形的性质可求得a的值，继而证明
， 根据相似三角形的性质即可求得答案.
(1)如图，过分别作交于点，交于点，则四边形是平行四边形，
四边形
是正方形，
，
，
，
平行四边形是正方形，
，
，
，
，
，
，
；
(2)由(1)得：，，
，
，，
，
，
，
，
；
(3)把绕点逆时针旋转得到，连接，
，
，
，
，
，
.
，，
，
，
是等腰直角三角形，
，
，
，
，
，
设，则，
在
中，
，则，
正方形的边长为
，
，
，
，
，
，
，
，
，
，
.
练习册系列答案
相关题目
