Question

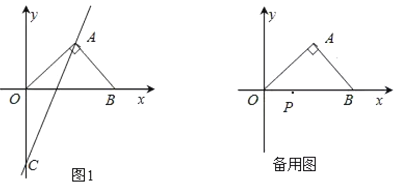
【题目】已知：在Rt△ABC中，∠ACB=90°，过点C作CD⊥AB于点D，点E是BC上一点，连接AE交CD于点F.

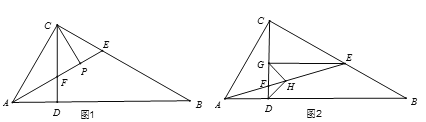
(1)如图1，若AE平分∠CAB，CP平分∠BCD，求证：FP=EP；

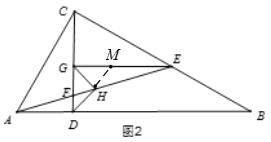
(2)如图2，若CE=CA，过点E作EG⊥CD于点G，点H为AE的中点，连接DH，GH，判断△GDH的形状，并证明.

Answer 1

【答案】(1)证明见解析；(2)△GDH是等腰直角三角形，理由见解析.

【解析】

(1)由CD⊥AB，∠ACB=90°可得∠ACD=∠B，继而根据角平分线的定义以及三角形外角的性质可得∠CFE=∠CEF，得到CF=CE，再根据等腰三角形的性质即可得证；

(2)如图2，延长DH交EG于点M，证明△ACD≌△CEG，从而可得AD=CG，CD=GE，再证明△ADH≌△EMH，从而可得EM=AD，DH=MH，继而根据CD=CG+DG，EG=EM+MG，可得DG=MG，判断出△DGM是等腰直角三角形，再根据DH=MH，可得HG⊥DH，GH=DH，从而可得△GDH是等腰直角三角形.

(1)∵CD⊥AB，∠ACB=90°，

∴∠ACD+∠CAD=90°，∠B+∠CAB=90°，

∴∠ACD=∠B，

∵AE平分∠CAB，

∴∠CAE=∠BAE，

∵∠CFE=∠ACD+∠CAE，∠CEF=∠B+∠BAE，

∴∠CFE=∠CEF，

∴CF=CE，

又∵CP平分∠BCD，

∴FP=EP；

(2)△GDH是等腰直角三角形，理由如下：

如图2，延长DH交EG于点M，

∵EG⊥CD，

∴∠CGE=∠EGD=90°，

∴∠CEG+∠ECG=90°，

∵∠ACD+∠ECG=∠ACB=90°，

∴∠ACD=∠CEG，

又∵∠ADC=90°=∠CGE，AC=CE，

∴△ACD≌△CEG，

∴AD=CG，CD=GE，

∵∠ACD=∠B，

∴∠CEG=∠B，

∴EG//AD，

∴∠HAD=∠HEG，∠ADH=∠EMH，

又∵AH=EH，

∴△ADH≌△EMH，

∴EM=AD，DH=MH，

∵CD=CG+DG，EG=EM+MG，

∴DG=MG，

∴△DGM是等腰直角三角形，

又∵DH=MH，

∴HG⊥DH，GH=DH，

∴△GDH是等腰直角三角形.