��Ŀ����
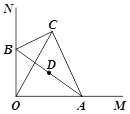
����Ŀ����ͼ��������y=ax2+bx+c������A����3��0����B��0��3����C��1��0����
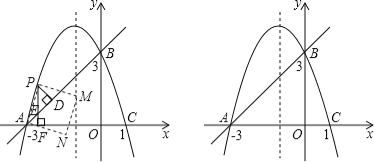
��1����������ߵĽ���ʽ��
��2����P��ֱ��AB�Ϸ�����������һ���㣬�������A��B�غϣ�������P��x��Ĵ��ߣ�����ΪF����ֱ��AB�ڵ�E����PD��AB�ڵ�D��
������P��ʲôλ��ʱ����PDE���ܳ���������ʱP������ꣻ
������PA����APΪ����ͼʾһ���������APMN�����ŵ�P���˶��������εĴ�С��λ��Ҳ��֮�ı䣮
������M��Nǡ�����������߶Գ�����ʱ�������Ӧ��P������꣮������������ţ�
���𰸡���1��y=��x2��2x+3����2������P��![]() ��
��![]() ��ʱ����PDE���ܳ��������������Mǡ�����������߶Գ�����ʱ����P����Ϊ��
��ʱ����PDE���ܳ��������������Mǡ�����������߶Գ�����ʱ����P����Ϊ��![]() ��
��![]() ����������Nǡ�����������߶Գ�����ʱ����P������Ϊ����
����������Nǡ�����������߶Գ�����ʱ����P������Ϊ����![]() ��1��2����
��1��2����
��������
�����������1���ѵ�A��B��C��������������߽���ʽ�����ô���ϵ��������κ�������ʽ�� �ɣ� ��2�������ݵ�A��B���������OA=OB���Ӷ��õ���AOB�ǵ���ֱ�������Σ����ݵ���ֱ�������ε����ʿɵ���BAO=45����Ȼ�������PED�ǵ���ֱ�������Σ����ݵ���ֱ�������ε����ʣ�PDԽ����PDE���ܳ�������жϳ�����ֱ��ABƽ�е�ֱ����������ֻ��һ������ʱ��PD��������ֱ��AB�Ľ���ʽΪy=x+3������ABƽ�е�ֱ�߽���ʽΪy=x+m���������߽���ʽ��������y���õ�����x��һԪ���η��̣����ø����б�ʽ��=0��ʽ���m��ֵ�������x��y��ֵ���Ӷ��õ���P�����ꣻ ����ȷ���������ߵĶԳ��ᣬȻ��i���ֵ�M�ڶԳ�����ʱ������P��PQ���Գ�����Q������ͬ�ǵ������������APF=��QPM�����������ǽDZ���֤����APF����MPQȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�PF=PQ�����P�ĺ�����Ϊn����ʾ��PQ�ij�����PF��Ȼ����������߽���ʽ���㼴�ɵý⣻��ii����N�ڶԳ�����ʱ��ͬ�������APF����ANQȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�PF=AQ�����ݵ�A�����������P�������꣬�ٴ��������߽���ʽ��������꣬���ɵõ���P�����꣮
�����������1����������y=ax2+bx+c������A����3��0����B��0��3����C��1��0����
�� ��
��
��� ��
��
���ԣ������ߵĽ���ʽΪy=��x2��2x+3��
��2���١�A����3��0����B��0��3����
��OA=OB=3��
���AOB�ǵ���ֱ�������Σ�
���BAO=45�㣬
��PF��x�ᣬ
���AEF=90�㩁45��=45�㣬
����PD��AB��
���PDE�ǵ���ֱ�������Σ�
��PDԽ����PDE���ܳ�Խ��
��ֱ��AB�Ľ���ʽΪy=x+3��
����ABƽ�е�ֱ�߽���ʽΪy=x+m��
���� ��
��
����y�ã�x2+3x+m��3=0��
����=32��4��1����m��3��=0��
��m=![]() ʱ��ֱ����������ֻ��һ�����㣬PD���
ʱ��ֱ����������ֻ��һ�����㣬PD���
��ʱx=![]() ��y=
��y=![]() +
+![]() =
=![]() ��
��
����P��![]() ��
��![]() ��ʱ����PDE���ܳ����
��ʱ����PDE���ܳ����
��������y=��x2��2x+3�ĶԳ���Ϊֱ��x=![]() ��
��
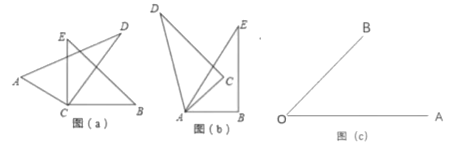
��i����ͼ1����M�ڶԳ�����ʱ������P��PQ���Գ�����Q��

��������APMN�У�AP=PM����APM=90�㣬
���APF+��FPM=90�㣬��QPM+��FPM=90�㣬
���APF=��QPM��
������APF����MPQ��
 ��
��
���APF�ա�MPQ��AAS����
��PF=PQ��
���P�ĺ�����Ϊn��n��0������PQ=��1��n��
��PF=��1��n��
����P��������n����1��n����
����P��������y=��x2��2x+3�ϣ�
����n2��2n+3=��1��n��
�����ã�n2+n��4=0��
���n1=![]() ����ȥ����n2=
����ȥ����n2=![]() ��
��
��1��n=��1��![]() =
=![]() ��
��
���ԣ���P������Ϊ��![]() ��
��![]() ����
����
��ii����ͼ2����N�ڶԳ�����ʱ���������߶Գ�����x�ύ�ڵ�Q��

�ߡ�PAF+��FPA=90�㣬��PAF+��QAN=90�㣬
���FPA=��QAN��
���ߡ�PFA=��AQN=90�㣬PA=AN��
���APF�ա�NAQ��
��PF=AQ��
���P����ΪP��x����x2��2x+3����
����x2��2x+3=��1������3��=2��
���x=![]() ��1���������⣬��ȥ����x=��
��1���������⣬��ȥ����x=��![]() ��1��
��1��
��ʱ��P����Ϊ����![]() ��1��2����
��1��2����
����������������Mǡ�����������߶Գ�����ʱ����P����Ϊ��![]() ��
��![]() ����������Nǡ�����������߶Գ�����ʱ����P������Ϊ����
����������Nǡ�����������߶Գ�����ʱ����P������Ϊ����![]() ��1��2����
��1��2����