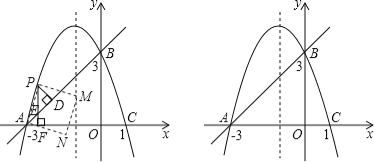题目内容
【题目】(1)如图(![]() ),将两块直角三角尺的直角顶点
),将两块直角三角尺的直角顶点![]() 叠放在一起
叠放在一起
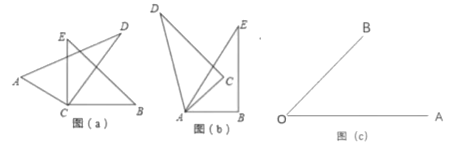
①若![]() ,则
,则![]() __________;若
__________;若![]() ,则
,则![]() ___________.
___________.
②猜想![]() 与
与![]() 的度数有何特殊关系,并说明理由.
的度数有何特殊关系,并说明理由.
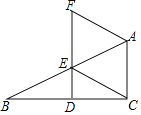
(2)如图(![]() ),两个同样的三角尺
),两个同样的三角尺![]() 锐角的顶点
锐角的顶点![]() 重合在一起,则
重合在一起,则![]() 与
与![]() 的度数有何关系?请说明理由.
的度数有何关系?请说明理由.
(3)如图(![]() ),已知
),已知![]() ,作
,作![]() (
(![]() ,
,![]() 都是锐角且
都是锐角且![]() ),若
),若![]() 在
在![]() 的内部,请直接写出
的内部,请直接写出![]() 与
与![]() 的度数关系.
的度数关系.
【答案】(1)①120°;40°②∠ACB+∠DCE=180°,理由见解析(2)∠DAB+∠CAE=120°,理由见解析(3)∠AOD+∠BOC=![]() 或∠AOD+∠BOC=
或∠AOD+∠BOC= ![]() 或∠BOC-∠AOD=
或∠BOC-∠AOD= ![]()
【解析】
(1)①先求出∠BCD,再代入∠ACB=∠ACD+∠BCD求出即可;先求出∠BCD,再代入∠DCE=∠BCE-∠BCD求出即可;
②根据∠ACB=∠ACD+∠BCD,∠DCE=∠BCE-∠BCD,利用角的加减化简即可
(2)先表示∠CAB、∠DAB,利用角的加减即可求解.
(3)分①OD在OB上方时②OD在∠BOC内部③OD在∠AOC内部④OD在OA下方4种情况进行讨论.
(1)①若∠DCE=60°
∵∠DCE=60°,∠ACD=∠BCE=90°
∴∠BCD=∠BCE-∠DCE=30°
∴∠ACB=∠ACD+∠BCD=120°;
若∠ACB=140°
∵∠ACB=140°,∠ACD=∠BCE=90°
∴∠BCD=∠ACB -∠ACD =50°
∴∠DCE=∠BCE-∠BCD=40°
故答案为:120°;40°
②猜想:∠ACB+∠DCE=180°,理由是:
∵∠ACD=∠BCE=90°
∴∠ACB=∠ACD+∠BCD=90°+∠BCD,∠DCE=∠BCE-∠BCD=90°-∠BCD
∴∠ACB+∠DCE=90°+∠BCD+90°-∠BCD=180°
(2)∠DAB+∠CAE=120°,理由是:
∵∠DAC=∠EAB=60°
∴∠DAB=∠DAC+∠CAB=60°+∠CAB,∠CAE=∠BAE-∠CAB=60°-∠CAB
∴∠DAB+∠CAE=60°+∠CAB+60°-∠CAB=120°
(3)①OD在OB上方时,如图:
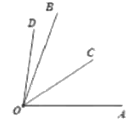
∠AOD+∠BOC=∠AOB+∠BOD+∠COD-∠BOD=∠AOB +∠COD=![]()
②OD在∠BOC内部,如图:
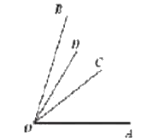
∠AOD+∠BOC=∠AOB-∠BOD+∠COD+∠BOD=∠AOB +∠COD=![]()
③OD在∠AOC内部,如图:
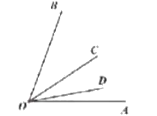
∠AOD+∠BOC=∠AOB-∠BOD +∠BOD-∠COD =∠AOB -∠COD=![]()
④OD在OA下方,如图:
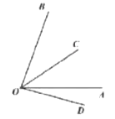
∠BOC-∠AOD= ∠AOB-∠AOC-(∠COD-∠AOC)=∠AOB -∠COD=![]()
综上所述:∠AOD+∠BOC=![]() 或∠AOD+∠BOC=
或∠AOD+∠BOC= ![]() 或∠BOC-∠AOD=
或∠BOC-∠AOD= ![]()

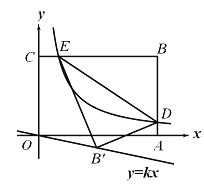
【题目】如图,点![]() 是菱形
是菱形![]() 边上的一个动点,点
边上的一个动点,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 的方向匀速运动到
的方向匀速运动到![]() 停止,过点
停止,过点![]() 作
作![]() 垂直直线
垂直直线![]() 于点
于点![]() ,已知
,已知![]() ,设点
,设点![]() 走过的路程为
走过的路程为![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为![]() (当点
(当点![]() 与点
与点![]() 或点
或点![]() 重合时,
重合时,![]() 的值为
的值为![]() )
)

小腾根据学习函数的经验,对函数随自变量的变化规律进行了探究,下面是小腾的探究过程,请补充完整;
(1)按照下表中自变量的值进行取点,画图,测量,分别得到了以下几组对应值;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,并画出函数的图像;
,并画出函数的图像;

(3)结合函数图像,解决问题,当点![]() 到直线
到直线![]() 的距离恰为点
的距离恰为点![]() 走过的路程的一半时,点P走过的路程约是
走过的路程的一半时,点P走过的路程约是 ![]()
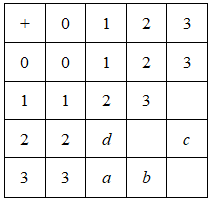
【题目】股民小明上星期六买进某公司股票1000股,每股20元,下表为本周内每日该股票的涨跌情况(单位.元)
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
每股 涨跌 | +4 | +4.5 | -1 | -2.5 | -5 | +2 |
(1)星期四收盘时,每股是多少元?
(2)本周内每股最高价多少元?最低价多少元?
(3)已知小明买进股票时付了2%0的手续费,卖出时还需付成交额2%0的手续费和1%0的交易税,如果小明在星期六收盘前将全部股票卖出,它的收益情况如何?(注:2%0=![]() )
)