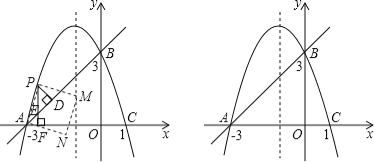��Ŀ����
����Ŀ�����������е�3������6��2��8���Ƚ��������ڵ��������������ұ�ȥ��ߵ���������֮��д����������֮�䣬�ɲ���һ���µ�������6��-4��2��6��8���Ϊ��һ�β��������ڶ���ͬ��������Ҳ�ɲ���һ����������6��-10��-4��6��2��4��6��2��8���������β�����ȥ���ʣ���������6��2��8��ʼ������2019�κ����������Ǹ���������������֮����( )
A.4054B.4056C.4058D.4060
���𰸡�A
��������
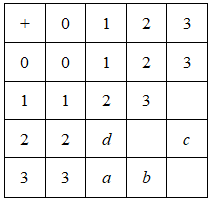
��ϲ���������ԭ�������ɵ�֪ÿ����һ�Σ�����֮�Ͷ�2���Ӷ��ó����ۣ�
��һ�β�����6��-4��2��6��8 ��ͽ����18
�ڶ��β���:6��-10��-4��6��2��4��6��2��8 ��ͽ����20
���������6��-16��-10��6��-4��10��6��-4��2��2��4��2��6��-4��2��6��8
��ͽ����22
����
��![]() �β�������ͽ����
�β�������ͽ����![]()
���2019�ν��Ϊ![]()
��ѡ��A

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ���ݡ��������������ܣ���2009��ʹ�����Ժ��ȽӴ������״�ͻ��1000���˴�֮��ÿ��Ӵ���������������2018��ͻ��1700���˴Σ���Ϊ�����ϽӴ������IJ���ݣ��ر������š����ڹʹ���������������ˣ��ʹ�����һ�������IJ���Ŀ�IJ�����������ٴ�����ʹ��ȣ����ǹʹ��Ĵ�Ӫ����ԱΪ������Բ�ͬ����Ⱥ����Ĵ���Ʒ����������˲��ֲι۹ʹ��Ĺ��ڵ����䣬����������������ͳ��ͼ����
2018��ι۹ʹ���������Ƶ���ֲ���
����x/�� | Ƶ��/���� | Ƶ�� |
20��x��30 | 80 | b |
30��x��40 | a | 0.240 |
40��x��50 | 35 | 0.175 |
50��x��60 | 37 | c |
�ϼ� | 200 | 1.000 |
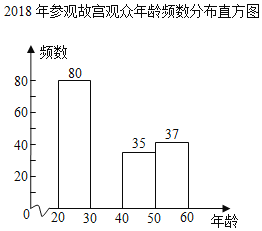
��1�������a��b��c��ֵ��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3���������Ͽ���������ڣ�20��x��40���Ѿ���Ϊ�ι۹ʹ�����ҪȺ�壮�������ι۹ʹ������ﵽ2000���˴Σ���ô�����������Ԥ��Լ�� ���˴Σ�
����Ŀ����ͼ����![]() ������
������![]() ���ϵ�һ�����㣬��
���ϵ�һ�����㣬��![]() �ӵ�
�ӵ�![]() ��������
��������![]() �ķ��������˶���
�ķ��������˶���![]() ֹͣ������
ֹͣ������![]() ��
��![]() ��ֱֱ��
��ֱֱ��![]() �ڵ�
�ڵ�![]() ����֪
����֪![]() �����
�����![]() �߹���·��Ϊ
�߹���·��Ϊ![]() ����
����![]() ��ֱ��
��ֱ��![]() �ľ���Ϊ
�ľ���Ϊ![]() ������
������![]() ���
���![]() ���
���![]() �غ�ʱ��
�غ�ʱ��![]() ��ֵΪ
��ֵΪ![]() ��
��

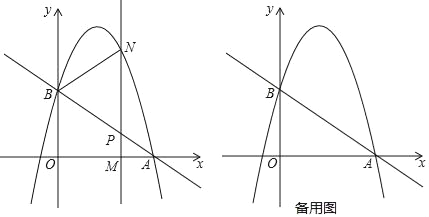
С�ڸ���ѧϰ�����ľ��飬�Ժ������Ա����ı仯���ɽ�����̽����������С�ڵ�̽�����̣��벹��������
��1�������±����Ա�����ֵ����ȡ�㣬��ͼ���������ֱ�õ������¼����Ӧֵ��
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
��2����ͬһƽ��ֱ������ϵ![]() �У������ȫ��ı��и�����ֵ����Ӧ�ĵ�
�У������ȫ��ı��и�����ֵ����Ӧ�ĵ�![]() ��������������ͼ��
��������������ͼ��

��3����Ϻ���ͼ������⣬����![]() ��ֱ��
��ֱ��![]() �ľ���ǡΪ��
�ľ���ǡΪ��![]() �߹���·�̵�һ��ʱ����P�߹���·��Լ��
�߹���·�̵�һ��ʱ����P�߹���·��Լ�� ![]()