题目内容
【题目】一船在灯塔
的正东方向
海里的
处，以20海里/时的速度沿北偏西
方向航行。
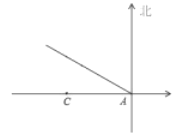
(1)多长时间后，船距灯塔最近？
(2)多长时间后，船到灯塔的正北方向？此时船距灯塔有多远？
【答案】（1）
小时船距灯塔最近；（2）
小时船在灯塔正北方向，此时船距灯塔8海里.
【解析】
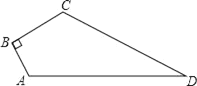
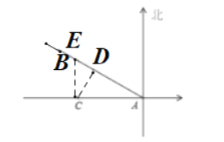
（1）过点C 作CD⊥AB 于D ，此时船与灯塔最近，根据含30°角的直角三角形的性质和勾股定理求出CD，然后根据“路程÷速度=时间”计算即可；
（2）过点C作CE⊥AC 交AB 于点E，构造直角三角形求得CE进而求得AE，然后根据“路程÷速度=时间”求出即可.
（1）
过点
作
于
，此时船与灯塔最近，
∵AC=
，∠DAC=90°-60°=30°，
∴
，AD=
=12，
（小时）
答：小时船距灯塔最近;
（2）过点作
交
于点
，则
，
解得
.
，
（小时）
答：小时船在灯塔正北方向，此时船距灯塔8海里.
练习册系列答案
阅读快车系列答案
相关题目
