题目内容
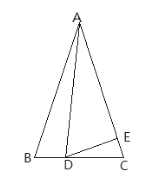
【题目】如图，已知在△ABC中，∠ABC=65°，AB=AC，∠BAD=20°，AD=AE，求∠EDC的度数.
【答案】∠EDC=10°
【解析】
根据△ABC为等腰三角形以及∠ABC的度数求出∠C和∠BAC的度数，根据∠BAD的度数得出∠DAE的度数，根据△ADE为等腰三角形求出∠AED的度数，最后根据△CDE的外角的性质求出∠EDC的度数．
∵∠ABC=65°，AB=AC∴∠B=∠C=65°（等边对等角）
∴∠BAC=180°-65°-65°=50°（三角形内角和180°）又∵∠BAD=20°
∴∠DAE=∠BAC-∠BAD=30°又∵AD=AE∴∠ADE=∠AED（等边对等角）
∴∠ADE=∠AED=（180°-∠DAE）÷2=75°（三角形内角和180°）
∵∠AED=∠EDC+∠C（三角形的一个外角等于与它不相邻的两个内角的和）
∴∠EDC=75°－65°=10°
练习册系列答案
名校课堂系列答案
相关题目
