Question

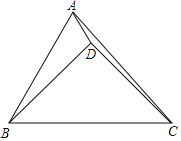
【题目】如图，四边形ABCD中，AB＝AD＝CD，以AB为直径的⊙O经过点C，连接AC，OD交于点E．

（1）证明：OD∥BC；

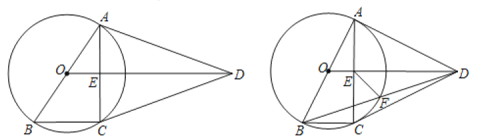
（2）若AD是⊙O的切线，连接BD交于⊙O于点F，连接EF，且OA＝1，求EF的长．

Answer 1

【答案】（1）见解析；（2）EF＝

【解析】

（1）连接OC，证明△ADO≌△CDO，根据全等三角形的性质得到∠AOD＝∠COD，由圆周角定理可证∠AOD=∠ABC，根据等腰三角形的性质得到∠OBC＝∠OCB，根据平行线的判定定理即可得到结论；

（2）连接AF，过F作FM⊥EF交OD于M，推出△ABD为等腰直角三角形，求得∠AFB＝90°，∠DAF＝∠45°，由△AEF≌△DMF可得AE＝DM，由△AOE∽DOA求出AE的长，进而可求EF的长．

解：（1）连接OC，

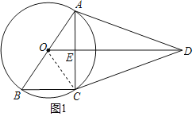
∵AO＝CO，AD＝CD，OD＝OD，

∴△ADO≌△CDO（SSS），

∴∠AOD＝∠COD，

∵∠AOC=2∠ABC，

∴∠AOD=∠ABC，

∵OB＝OC，

∴∠OBC＝∠OCB，

∴∠OCB＝∠COD，

∴OD//BC；

（2）连接AF，过F作FM⊥EF交OD于M，

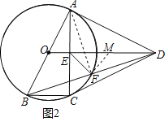
∵AB＝AD，AD是圆的切线，

∴△ABD为等腰直角三角形，

∵AB为直径，

∴∠AFD＝90°，∠DAF＝∠45°，

∵∠AED＝∠AFD＝90°，

∴∠DAF＝∠DEF＝45°，

∴AF＝DF，

∴∠AFE＝∠DFM，

∵∠EAF＝∠FDM，

∴△AEF≌△DMF（ASA），

∴AE＝DM．

∵OA＝1，

∴AD=2，

∴OD=，

∵∠AOE=∠AOD，∠AEO=∠OAD，

∴△AOE∽DOA，

∴ ，

∴AE=，

∴DM＝，

∴DE＝，

∴EM＝，

∴EF＝．